Йэн Стюарт - Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres]

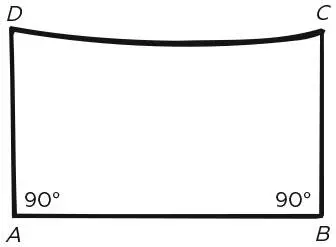
Четырехугольник Саккери: сторона CD нарочно сделана кривой, чтобы избежать евклидовых заключений об углах C и D

Ученый начал с гипотезы для тупых углов и через ряд теорем вывел – как ему казалось, – что углы C и D должны в конце концов оказаться прямыми. Это противоречие, а значит, гипотеза для тупых углов ошибочна. Затем Саккери перешел к острым углам, что потребовало нового ряда теорем, причем все они были верны и любопытны сами по себе. Попутно ученый доказал довольно сложную теорему о семействе линий, проходящих через одну общую точку, в которой говорилось, что две из этих линий будут иметь общий перпендикуляр в бесконечности. На самом деле это не противоречие, хотя Саккери думал именно так и объявил гипотезу для острых углов также опровергнутой.

Оставался единственный вариант – с геометрией Евклида, и Саккери счел свою задачу выполненной. Но другие ученые заметили, что на самом деле никакого противоречия из гипотезы для острого угла не было, появилась лишь очередная удивительная теорема. И к 1759 г. д’Аламбер объявил статус пятого постулата: «скандал с началами геометрии».

К 1813 г. Гаусс успел окончательно убедиться, что антиевклидова, затем астральная и, наконец, неевклидова геометрия логически возможны. Он задался вопросом, что тогда можно считать истинной геометрией пространства, и измерил углы треугольника, образованного тремя горами в Нижней Саксонии: Броккен, Хохехаген и Инзельберг. Чтобы результаты не искажались кривизной Земли, в измерениях он использовал местную плоскость горизонта. Сумма измеренных им углов оказалась на 15 угловых секунд больше 180°. По всему выходило, что это тупой угол, но возможность ошибки в наблюдениях сводила на нет всю ценность опыта. Гауссу требовался гораздо больший треугольник и более точные инструменты для измерения углов.

Немецкий математик Георг Клюгель прочел книгу Саккери и выразил новаторское и даже несколько шокирующее мнение, что убежденность в правоте пятого постулата относится скорее к области опыта, чем логики. Он утверждал, что некая особенность нашего образа мышления и представления о пространстве заставляет нас верить в существование параллельных линий со свойствами, которые описал Евклид.

В 1776 г. Иоганн Ламберт, следуя предположению Клюгеля, занялся исследованиями, похожими на работу Саккери, но он начал с четырехугольника с тремя прямыми углами. Четвертый угол у него мог быть или прямым (евклидова геометрия), или тупым, или острым. Как и Саккери, он предположил, что тупой угол приводит к противоречию. Точнее, он решил, что это приводит к сферической геометрии, где давно известно, что сумма углов четырехугольника больше 360°, поскольку сумма углов треугольника больше 180°. Раз сфера – это не плоскость, вариант с тупым углом исключался.

Однако Ламберт ничего подобного не утверждал для острого угла. Зато он доказал ряд любопытных теорем, однако самой блестящей оказалась выведенная им формула вычисления площади многоугольника с n сторонами. Сложите все углы и вычтите их из суммы 2 n – 4 прямых углов: результат окажется пропорциональным площади многоугольника. Эта формула напомнила Ламберту похожую из сферической геометрии: сложите все углы и вычтите 2 n – 4 прямых угла: результат снова окажется пропорциональным площади многоугольника. Разница несущественна: вычитание выполняется в обратном порядке. Ученый подошел вплотную к неясному, но пророческому утверждению: геометрия острого угла такая же, как у сферы с мнимым радиусом .

Ламберт тут же написал короткую статью о тригонометрических функциях мнимых углов, выведя несколько изящных и идеально согласующихся формул. Теперь мы признаём эти функции: это так называемые гиперболические функции, которые можно вычислить, не прибегая к мнимым числам, и они удовлетворяют всем формулам Ламберта. Было очевидно, что за его неожиданным, загадочным предположением кроется что-то интересное. Но что?

К определенному моменту у наиболее информированных геометров сложилось твердое убеждение в том, что пятый постулат Евклида не может быть доказан с помощью остальных аксиом. Случай с острым углом оказался слишком логичным, чтобы привести к противоречию. С другой стороны, сфера с мнимым радиусом тоже не выглядела достаточно солидно, чтобы подкрепить это убеждение.

Одним из таких геометров был Гаусс, с юности веривший в вероятность существования логически последовательной неевклидовой геометрии и позже доказавший в этой области немало теорем. Но, как он откровенно заявил в 1829 г. в письме к Бесселю, у него не было намерения публиковать некоторые из своих работ из опасения стать объектом того, что он называл «криками беотийцев». Люди, лишенные воображения, не смогут его понять и в своем невежестве и приверженности традициям поднимут его на смех. Возможно, в этом опасении ученый укрепился из-за излишнего почтения к философскому авторитету Канта: тот утверждал, что геометрия пространства должна быть евклидовой.

В 1799 г. Гаусс написал венгерскому ученому Фаркашу Бойяи, признавшись, что его исследование «заставит меня сомневаться в истинности геометрии. Да, я добился того, что многие уверенно назвали бы доказательством (пятого постулата с помощью других аксиом), но в моих глазах это всё ничего не стоит».

Прочие математики оказались не столь щепетильными. В 1826 г. Николай Лобачевский уже читал в Казанском университете лекции по неевклидовой геометрии. Он ничего не знал о работах Гаусса, но доказал те же теоремы своими методами. Две статьи на эту тему появились в 1829 и 1835 гг. Никакого шума, как опасался Гаусс, они не подняли, скорее, без следа канули в неизвестность. В 1840 г. Лобачевский опубликовал книгу на ту же тему, где открыто посетовал на отсутствие интереса. В 1855 г. он выпустил новый труд, развивавший достижения первого.

Независимо от них сын Фаркаша Бойяи, Янош, армейский офицер, пришел к тем же идеям в 1825 г. и изложил их в 26-страничном труде, опубликованном в книге его отца по геометрии «Опыт введения учащегося юношества в начала чистой математики» как приложение в 1832 г. Он признавался отцу: «Я сделал открытия столь поразительные, что сам растерялся».

Гаусс прочел эту работу, но объяснил Фаркашу, что не считает себя вправе хвалить молодого ученого, потому что «оценить это – всё равно что оценить себя». Возможно, это было не совсем справедливо, но таков уж был этот человек.