Йэн Стюарт - Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres]

1 + 2 – s + 3 – s + 4 – s + …

равен произведению, по всем простым р , следующего ряда:

1 + p – s + p –2 s + p –3 s + … = 1/(1 – p – s ).

Здесь мы должны взять s > 1, чтобы ряд сходился.

В 1848 г. Пафнутий Чебышёв добился некоторого прогресса в доказательстве предположения Гаусса, используя комплексную функцию, родственную рядам Эйлера и позже названную дзета-функцией ζ( z ). Роль ее полностью осветил Риман в 1859 г. в своей статье «On the Number of Primes Less Than a Given Magnitude» («О числе простых чисел, не превышающих заданной величины»). Он показал, что статистические свойства простых чисел тесно связаны с нулями дзета-функции, т. е. решениями z уравнения ζ( z ) = 0.

В 1896 г. Жак Адамар и Шарль де ла Валле-Пуссен использовали дзета-функцию для доказательства теоремы о распределении простых чисел. Главной трудностью было показать, что ζ( z ) не равна 0 для всех z вида 1 + it . Чем лучше мы контролируем расположение нулей дзета-функции, тем больше узнаем о простых числах. Риман предположил, что все нули, за исключением тривиальных (получающихся при z , равной отрицательным четным целым числам), расположены на критической прямой z = 1/ 2+ it .

В 1914 г. Харди доказал, что на этой прямой располагается бесконечное множество нулей. Мощные компьютерные данные позже подтвердили эту гипотезу. Себастьян Веденивский с помощью компьютерной программы ZetaGrid в 2001–2005 гг. удостоверил, что первые 100 миллиардов нулей лежат именно на критической прямой.

Гипотеза Римана отмечена номером 8 в знаменитом списке нерешенных кардинальных математических задач, составленном Давидом Гильбертом и содержащем 23 пункта. Кроме того, это одна из задач тысячелетия, за решение которой Математический институт Клея предлагает миллион долларов.

Первопроходцы в области исчисления с кавалерийской отвагой оперировали бесконечностью. Эйлер предположил, что степенные ряды подобны многочленам, и использовал эту гипотезу с сокрушительным эффектом. Но в руках простых смертных такого рода наскоки легко могут привести к откровенной глупости. Даже сам Эйлер иногда высказывал неумные мысли. Например, он начал со степенного ряда 1 + x + x 2+ x 3+ x 4+ …, чья сумма равна 1/(1 – x), положил x = –1 и вывел:

1-1 + 1–1 + 1–1 + … = 1/ 2,

что является бессмыслицей. Степенные ряды не сходятся, если x не расположен строго между –1 и 1, что прояснила теория Вейерштрасса.

И только беспощадная критика, подобная той, что высказал епископ Беркли, в итоге обогатила математику и поставила ее на прочную основу. Благодаря этому сложился принцип: чем сложнее твое построение, тем важнее заручиться для него безукоризненным основанием.

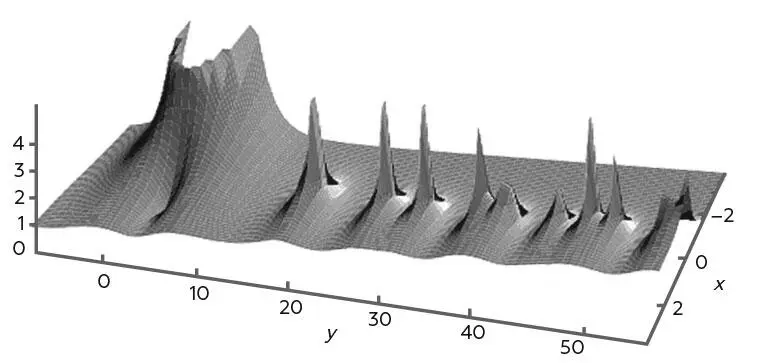
Модуль дзета-функции Римана

В наши дни большинство пользователей математики снова пренебрегают ее тонкостями, будучи уверенными в том, что знания, которые они применяют и которые им кажутся разумными, вероятно, имеют строгое обоснование. В этой самоуверенности их укрепили открытия Больцано, Коши и Вейерштрасса. Тем временем профессиональные математики продолжали разрабатывать строгие концепции бесконечности. Даже появилось движение, ратовавшее за возвращение концепции бесконечно малой величины (флюксии), известное как нестандартный анализ, который является совершенно строгим и технически полезным для некоторых других малоподатливых проблем. Здесь удалось избежать логических нестыковок, провозгласив бесконечно малые новым видом чисел, а не условным действительным числом. По духу это близко к тому, как думал Коши. Нестандартный анализ – удел узких специалистов, но, возможно, он станет методом будущего.

Анализ используется биологами для изучения динамики роста популяций различных организмов. Простым примером может служить логистическое отображение, или модель Ферхюльста – Пирла. Здесь изменение величины популяции x является функцией от времени t , моделируемой дифференциальным уравнением:

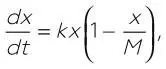
где константа М является «пропускной способностью», максимальной величиной популяции, которую может поддерживать окружающая среда.

Стандартный аналитический метод предлагает точное решение

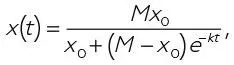
которое называется логистической кривой. Соответственно модели численность популяции начинает расти очень быстро (экспоненциально), но по мере приближения величины популяции к половине пропускной способности кривая постепенно выравнивается, пока не достигает уровня пропускной способности.

Эта кривая не может точно отражать реальность, хотя достаточно четко воспроизводит поведение многих популяций. Более сложные модели такого типа представят данные, сильнее приближенные к реальности. Потребление человеком природных ресурсов также можно смоделировать в виде логистических кривых, обеспечивая возможность оценить потребности в этих ресурсах в будущем, а также сроки, на которые их хватит.

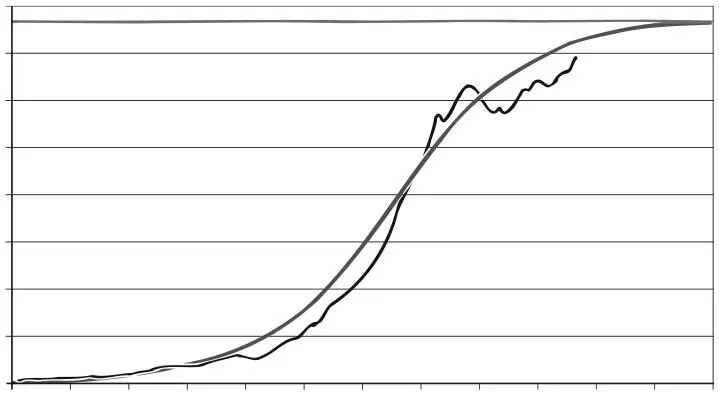
Мировое потребление нефти-сырца с 1900 по 2000 г.: сглаженная кривая – данные анализа, неровная кривая – реальные данные

В основу исчислениялегли принципы геометрии, но и сама она была сокращена до символических вычислений, которые затем формализовались в анализ. Однако наглядное мышление по-прежнему важно для развития математики, особенно в одном новом и даже поначалу шокирующем направлении. На протяжении более 2000 лет имя Евклида было синонимом геометрии. Последователи успешно развивали его идеи, особенно в области конических сечений, но никто из них так и не внес радикальных изменений в основания дисциплины. Убеждение в том, что в мире существует лишь одна геометрия, евклидова, и строгое математическое описание пространства возможно лишь на его принципах, только укреплялось. Люди с трудом могли даже помыслить о какой-то альтернативе.

Так не могло продолжаться вечно.

Первое значительное отступление от правил евклидовой геометрии зародилось в недрах самого что ни на есть практического ее применения – навигации. На коротких расстояниях Земля может считаться практически плоской, и ее географические особенности можно точно перенести на плоскость. Но по мере того, как корабли совершали всё более длительные путешествия, учитывать истинную форму нашей планеты стало жизненно необходимо. Некоторые древние цивилизации знали, что Земля круглая. Доказательств было немало: начиная с того, как исчезает на горизонте уплывающий корабль, и кончая тенью планеты, падающей на Луну во время затмений. Это наталкивало древних ученых на мысль, что Земля – идеальный шар.