Йэн Стюарт - Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres]

Мало-помалу математики XIX в. научились разделять разные концептуальные вопросы в этой сложнейшей области. Первым стало значение самого термина «функция». Вторым – разные способы представления функций: в виде формулы, степенного ряда, ряда Фурье и т. д. Третий вопрос – какими свойствами обладают функции. Четвертый – какое представление функции гарантирует эти свойства. Простой многочлен, например, определяет непрерывную функцию. А обычный ряд Фурье, судя по всему, нет.

Очень быстро анализ Фурье превратился в тест для самой идеи функции. Это обострило проблемы, и важность приобрели скрытые различия технических приемов. Не кто иной, как Дирихле, в 1837 г. предложил современное определение функции в статье, посвященной рядам Фурье. В результате он согласился с Фурье: переменная y является функцией другой переменной x , если для каждого значения x (в определенном диапазоне) задано единственное значение y . Он недвусмысленно утверждал, что здесь не нужны специальный закон или формула – достаточно, чтобы у можно было определить некой четко прописанной последовательностью математических действий, примененных к x . На тот момент должен был казаться экстремальным пример, приведенный им ранее, а именно в 1829 г.: функция f ( x ) принимает одно значение, когда x – рациональное число, и другое, когда x – иррациональное. Эта функция разрывная в каждой своей точке. (В наше время функции, подобные этой, рассматриваются как довольно невинные, так как возможно гораздо худшее поведение.)

Для Дирихле квадратный корень не был одной двузначной функцией. Это были две однозначные функции. Для действительного x это естественно – но не существенно: взять положительный квадратный корень как одну из них и отрицательный как другую. Для комплексных чисел нет очевидного естественного выбора, хотя какое-то число решений можно найти, чтобы облегчить жизнь.

У математиков до сих пор есть привычка: несмотря на великое множество определений понятия «функция», они всё равно то и дело открывают у нее еще какие-то качества, выходящие за рамки определения. В частности, они предположили, что любая разумная формула, например многочлен, автоматически определяет непрерывную функцию. Однако они никогда не доказывали этого – и прежде всего потому, что не определили термин «непрерывная». По большей части данная область всё еще находилась под властью интуитивных построений, отнюдь не всегда правильных.

Первым начал серьезно разбираться в этом беспорядке священник из Богемии, философ и математик Бернард Больцано. Он подвел надежный логический фундамент под большинство основных идей исчисления; главным исключением было то, что он принял как данность существование действительных чисел. Он настаивал, что бесконечно малые и бесконечно большие величины не существуют, а значит, не могут быть использованы, как бы соблазнительно это ни выглядело. И он же дал первое вразумительное определение непрерывной функции. А именно: f непрерывна, если разница f ( x + a ) – f ( x ) может быть настолько малой, насколько мы пожелаем, если а тоже достаточно мала. Предыдущие авторы предпочитали формулировки вроде «если а сколь угодно малая величина, то f ( x + a ) – f ( x ) также сколь угодно мала». Но для Больцано а была всего лишь числом, подобным другим. Он рассуждал так: каким бы малым ни было f ( x + a ) – f ( x ), вы всё равно должны найти для него соответствующую величину а . Не было необходимости, чтобы одна и та же величина использовалась каждый раз.

Например, f ( x ) = 2 x непрерывна, потому что 2( x + a ) – 2 x = 2 a . Если вы хотите, чтобы 2 а было меньше определенного числа, скажем 10 –10, вам нужно сделать а меньше 10 –10/2. Если вы возьмете более сложную функцию, скажем f ( x ) = x 2, вычисления будут немного сложнее, потому что правильное значение а зависит от x так же, как и от выбранной нами величины, 10 –10, но любой опытный математик решит эту задачу за пару минут. Пользуясь таким определением, Больцано доказал – впервые в истории, – что полиномиальная функция непрерывна. Но на протяжении 50 лет до этого никому не было дела. Больцано опубликовал свою работу в журнале, который вообще не мог попасть в руки математика – не то чтобы его заинтересовать. В наши дни господства интернета в это трудно поверить, но еще 50 лет назад средства коммуникации не шли ни в какое сравнение с нашими. Что уж говорить о периодике 180-летней давности?

В 1821 г. Коши пришел практически к тому же выводу, но использовал несколько путанную терминологию. Его определение непрерывности функции f заключалось в том, что разница между f ( x ) и f ( x + а ) бесконечно мала, если бесконечно мала величина а , что на первый взгляд кажется старым, плохо определенным подходом. Однако бесконечно малой величиной для Коши было не отдельное число, почему-то бесконечно малое, а постоянно убывающая последовательность чисел. Например, последовательность 0,1, 0,01, 0,001, 0,0001 и т. д. бесконечно мала в понимании Коши, но каждое отдельное число, например 0,0001, – обычное действительное число. Возможно, малое, но не бесконечно. Учитывая терминологию, мы видим, что концепция непрерывности Коши в точности повторяет Больцано.

Очередным критиком недостатков в изучении бесконечных процессов стал Абель, жаловавшийся на то, что ученые используют бесконечные ряды, не дав себе труда поинтересоваться, имеет ли смысл их сумма. Его критика оказалась действенной, и мало-помалу в хаосе стали намечаться черты некоего порядка.

Расцвет математической физики в XIX в. был ознаменован открытием ряда важнейших дифференциальных уравнений. Не имея современных высокоскоростных компьютеров, способных находить численные решения, математики того времени изобрели для уравнений новые специальные функции. И они работают по сей день. Примером может служить уравнение Бесселя . Первым его вывел Даниил Бернулли, а позже обобщил Бессель. Вот оно:

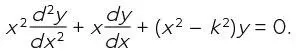
Здесь обычные функции, такие как экспонента, синус, косинус или логарифм, не помогут найти решение. Но можно воспользоваться методами анализа в виде степенного ряда. Он определяет новые функции, так называемые функции Бесселя. Простейшая функция Бесселя обозначается как J k( x ); но есть и другие. Степенные ряды позволяют вычислить J k( x ) с необходимой точностью.