Йэн Стюарт - Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres]

После революции 1830 г. Коши ненадолго эмигрировал в Швейцарию, а в 1831 г. стал профессором теоретической физики в Турине. Как преподаватель он проявил себя крайне неорганизованным. В 1833 г. он перебрался в Прагу, став преподавателем у внука Карла X. Однако принцу были одинаково противны как математика, так и физика, отчего Коши часто выходил из себя. Ученый вернулся в Париж в 1838 г., восстановился в качестве преподавателя в Академии, но не хотел преподавать, пока в 1848 г. не был низложен Луи-Филипп I. За свою научную карьеру Коши успел опубликовать 789 блестящих работ по математике.

Эта теорема касается определенных интегралов от комплексных функций, т. е. выражения:

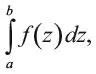
где a и b – комплексные числа. В вещественном анализе это выражение можно оценить, найдя первообразную F ( z ) для f ( z ), т. е. такую функцию F ( z ), чтобы ее производная dF ( z )/ dz = f ( z ). Тогда определенный интеграл равен F ( b ) – F ( a ). В данном случае его величина зависит только от конечных точек a и b , а не от того, как вы движетесь от одной к другой.

В комплексном анализе, по словам Гаусса, всё иначе. Здесь величина интеграла может зависеть от пути , по которому переменная z движется от точки a к точке b. Поскольку комплексные числа формируют плоскость, их геометрия гораздо богаче, чем у вещественной прямой, и здесь очень важны дополнительные характеристики.

Например, представим, что вы интегрируете f ( z ) = 1/ z от a = –1 до b = 1. Если упомянутый путь представляет собой полуокружность P , расположенную выше вещественной оси, то интеграл получается равным –π i . Но если путь представляет собой полуокружность Q , расположенную ниже вещественной оси, интеграл будет равен π i . Это две разные величины, и разница между ними равна 2π i .

По мнению Гаусса, разница появляется, потому что функция 1/ z ведет себя плохо. Она делается бесконечной в зоне, ограниченной двумя путями, а именно в точке z = 0, которая является центром окружности, образованной двумя путями. «Я утверждаю теперь, что интеграл ‹…› сохраняет одно и то же значение, если внутри части плоскости, заключенной между двумя путями, представляющими переход, функция нигде не равна бесконечности. Это прекрасная теорема, и доказательство к ней я при случае предоставлю». Однако последнего Гаусс так и не сделал.

Теорема была вновь открыта другим ученым, Огюстеном Луи Коши, подлинным основателем комплексного анализа. Да, Гаусс высказал много блестящих идей, но они бесполезны, пока лежат под спудом. Коши опубликовал свою работу. Он постоянно публиковал что-то новое. Говорят, что журнал Comptes Rendus de l’Academie Française принял негласное правило (действующее по сей день) не принимать статьи длиннее четырех печатных страниц как раз ради того, чтобы не позволить Коши заполонить все страницы. Но даже это не обескуражило ученого: он стал писать больше коротких статей. Основные принципы комплексного анализа с удивительной скоростью вылетали из-под его неутомимого пера. И он оказался гораздо более простой, изящной и во многом более полной теорией, чем вещественный анализ.

Например, в вещественном анализе функция может быть дифференцируемой, а ее производная – нет. Она может быть дифференцируемой 23 раза, а на 24-й – нет. Она может быть дифференцируема столько раз, сколько вам угодно, но не может быть представлена степенным рядом. Ни одна из этих неприятностей не грозит вам в комплексном анализе. Если функция дифференцируема, ее можно дифференцировать сколько угодно раз; более того, она может быть представлена степенным рядом. Причина – в тесном взаимодействии с теоремой Коши и, возможно, тем фактом, который Гаусс всё же применил в своем тайном доказательстве: чтобы быть дифференцируемой, комплексная функция должна отвечать очень жестким стандартам, известным как условия Коши – Римана . Эти условия прямо приводят нас к результатам Гаусса, что интеграл между двумя точками может зависеть от выбранного пути. Соответственно, как отмечал Коши, интеграл по замкнутому пути не может не равняться 0. Он равен 0 при условии, что данная функция дифференцируема (в этом случае она не бесконечна) в любой точке на пути.

Была открыта теорема о вычетах, которая позволяет вычислить величину интеграла вокруг замкнутого пути, зависящую только от расположения этих точек, где функция становится бесконечной, а также поведение функции вблизи этих точек. В двух словах: сама структура комплексной функции определяется ее особыми точками, в которых она себя «плохо» ведет. А самые важные точки – полюсы , где функция становится бесконечной.

Квадратный корень из –1 ставил в тупик математиков на протяжении столетий. Хотя, похоже, такой величины и не было, она использовалась в расчетах. Были намеки на то, что сама по себе идея должна иметь какой-то смысл, поскольку может быть использована для получения достоверных результатов, которые сами по себе не связаны с квадратным корнем из отрицательного числа.

Поскольку успешное использование этой невозможной величины продолжало развиваться, математики стали активно ее применять. Ее статус оставался неопределенным, пока не стало очевидно существование логически последовательного расширения традиционной системы действительных чисел, в которой √–1 – не более чем новая грань числа, подчиняющаяся всем привычным законам арифметики.

В наши дни комплексные числа широко применяются и в физике, и в инженерии. Простой пример – изучение колебаний – периодически повторяющихся движений. Вспомним колебания здания во время землетрясения, вибрации в движущемся автомобиле или передачу по проводам переменного тока.

Простейший и основной вид колебаний описывается выражением a cos ω t , где t – время, a – амплитуда колебаний, а ω – их частота. Удобно преобразовать эту формулу как действительную часть комплексной функции e i ω t . Использование комплексных чисел упрощает подсчеты, поскольку экспонента проще косинуса. Поэтому инженеры, изучающие колебания, предпочитают работать с комплексными экспонентами и обращаются к их действительной части только в самом конце вычислений.

Комплексные числа также определяют устойчивость стационарных состояний динамических систем и широко применяются в теории управления. Это отрасль науки, посвященная методам стабилизации систем, иначе остающихся нестабильными. Пример – использование контролируемых компьютером подвижных управляемых панелей, стабилизирующих в полете положение космического шаттла. Без такого приложения комплексного анализа шаттлы попадали бы с неба, как кирпичи.