Йэн Стюарт - Укрощение бесконечности. История математики от первых чисел до теории хаоса [litres]

Функции Бесселя естественным образом возникают в задачах, связанных с кругами и цилиндрами, такими как колебание круглой мембраны, распространение электромагнитных волн в цилиндрическом волноводе, теплопроводность в цилиндрическом металлическом стержне и физика лазеров.

Интенсивность лазерного излучения описывается функцией Бесселя J 1( x )

Идеи Больцано дали толчок дальнейшему усовершенствованию. Он сделал возможным определение предела бесконечной последовательности чисел и, следовательно, ряда, который является суммой бесконечной последовательности. Так, его формализм подразумевает:

1 + 1/ 2+ 1/ 4+ 1/ 8+ 1/ 16+ …

и т. д. до бесконечности. Это осмысленная сумма, и ее величина точно равна 2. Не чуть-чуть меньше, не бесконечно малой величине меньше 2, а ровно 2. Чтобы понять, как это работает, предположим, что у нас есть последовательность чисел:

a 0, a 1, a 2, a 3, …

и т. д. до бесконечности. Мы можем сказать, что a nстремится к пределу a по мере того, как n стремится к бесконечности, если для любого числа ε > 0 существует такое число N , что разница между a nи а меньше, чем ε, для любого n > N . (Символ ε, один из традиционно используемых математиками, – греческая буква эпсилон.) В этом определении все числа конечные – никаких бесконечно малых или бесконечно больших. В дополнение к бесконечному ряду выше взглянем на его конечные суммы:

a 0= 1,

a 1= 1 + 1/ 2= 3/ 2,

a 2= 1 + 1/ 2+ 1/ 4= 7/ 4,

a 3= 1 + 1/ 2+ 1/ 4+ 1/ 8= 15/ 8

и т. д. Разница между a nи 2 равна 1/2 n. Чтобы сделать ее меньше ε, мы берем n > N = log 2( 1/ ε).

Ряд, имеющий конечный предел, называют сходящимся. Конечная сумма определяется как предел последовательности конечных сумм, полученных добавлением всё новых ее элементов. Если такой предел существует, ряд сходящийся. И производные, и интегралы – лишь разновидности пределов. Они существуют – иными словами, обретают математический смысл – при условии, что их пределы сходятся. Пределы, как отмечал Ньютон, – некая величина, которая позволяет определить, как некое другое число приближается к бесконечности или 0. Но при этом число не может достичь бесконечности или 0.

Сегодня исчисление в целом опирается на непоколебимый фундамент. Ранее его главным недостатком было то, что, прежде чем прибегнуть к поиску предела, никто не интересовался, есть ли вообще сходимость. Лучшим способом сделать это было бы доказательство еще нескольких более общих теорем о том, какие виды функций непрерывны, или дифференцируемы, или интегрируемы, и какие последовательности и ряды сходятся. Именно этим и занялись математики, и именно поэтому мы можем уже не тревожиться из-за нестыковок, отмеченным епископом Беркли. Поэтому мы больше не противимся использованию рядов Фурье: теперь можно точно определить, когда они сходятся, а когда нет, и уж, во всяком случае, четко понять, в каком смысле они сходятся. Существует достаточно возможностей выбрать тот ряд Фурье, который вам нужен.

Вейерштрасс открыл, что одинаковые идеи работают и с комплексными числами, и с действительными. Любое комплексное число z = x + iy имеет модуль 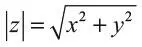, что, согласно теореме Пифагора, равно расстоянию от 0 до z на комплексной плоскости. Если мерить величину комплексного выражения с помощью его модуля, то определения предела, ряда и т. п., сформулированные для действительных чисел еще Больцано, тут же перенесутся в область комплексного анализа.

Вейерштрасс отметил, что один особый вид бесконечного ряда кажется особенно полезным. Он известен как степенной ряд и выглядит как многочлен бесконечной степени:

f ( z ) = a 0+ a 1 z + a 2 z 2+ a 3 z 3+ …,

где коэффициенты a n – конкретные числа. Вейерштрасс углубился в исследование этого вопроса, стремясь полностью провести комплексный анализ степенных рядов. Результаты вышли блестящими.

Например, вы можете описать экспоненциальную функцию выражением:

e z= 1 + z + 1/ 2 z 2+ 1/ 6 z 3+ 1/ 24 z 4+ 1/ 120 z 5+ …,

где 2, 6, 24, 120 и т. д. являются факториалами – произведениями последовательности целых чисел (например, 120 = 1 × 2 × 3 × 4 × 5). Эвристически Эйлер уже выводил эту формулу, теперь же Вейерштрасс получил ее логическим путем. В очередной раз использовав страницы из книги Эйлера, он сумел преобразовать тригонометрические функции в экспоненциальные, определив:

cos θ = 1/ 2( e i θ+ e – i θ),

sin θ = 1/ 2 i( e i θ – e – i θ).

Все стандартные свойства этих функций вытекают из их выражений в виде степенного ряда. Вы даже можете определить π и доказать, что e i π= –1, как утверждал Эйлер. И из этого, в свою очередь, вытекает, что комплексные логарифмы ведут себя именно так, как описывал Эйлер. Всё это наполнилось смыслом. Комплексный анализ перестал быть загадочным продолжением вещественного анализа: он превратился в самостоятельный серьезный предмет. На поверку вышло, что подчас работать в комплексной области даже проще, чтобы выразить в конце вещественный результат.

По Вейерштрассу, все эти достижения были лишь началом – первым этапом грандиозной программы. Но главное – были получены правильные основания. Теперь математики могли без опасений продолжать строить всё более сложное здание нового раздела науки.

Вейерштрасса отличал поразительно светлый ум, открывавший ему путь в самых сложных хитросплетениях пределов, производных и интегралов. И он не сбивался с выбранного курса. Также он заранее видел потенциально трудные места. Одна из его самых удивительных теорем доказывала, что существует функция f ( x ) от действительной переменной x , непрерывная в любой точке, но не дифференцируемая ни в одной точке. Графиком такой функции является непрерывная кривая, но ее изгибы так прихотливы, что мы не можем провести ни одну касательную к ней. Его предшественники не верили в такую возможность, современники недоумевали, к чему ведет такая теорема. А его последователи развили теорему в самую захватывающую новую теорию ХХ в. – теорию фракталов.

Но об этом мы поговорим позже.

Самой известной нерешенной проблемой для всех математиков является гипотеза Римана: вопрос комплексного анализа, возникший в связи с простыми числами, отразился в итоге на всей математике.

Примерно в 1793 г. Гаусс предположил, что количество простых чисел, меньших х , приблизительно равно x /ln x . На самом деле он сделал более точное приближение, названное интегральным логарифмом. В 1737 г. Эйлер отметил многообещающую связь между теорией чисел и анализом: бесконечный ряд