Авинаш Диксит - Стратегические игры
- Название:Стратегические игры
- Автор:
- Жанр:
- Издательство:Манн, Иванов и Фербер
- Год:2017
- Город:Москва
- ISBN:9785001008132
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Авинаш Диксит - Стратегические игры краткое содержание
Книга будет полезна как интересующимся математикой и ее применением в бизнесе и в жизни, так и тем, кто хочет развить стратегическое мышление и научиться принимать обоснованные решения.
Стратегические игры - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
U10 (дополнительное упражнение).Выполните упражнение S11, исходя из предположения о том, что BMA — компания с низким уровнем затрат с вероятностью 0,6.
U11 (дополнительное упражнение).Выполните упражнение S11, исходя из предположения, что в компании BMA с низким уровнем издержек затраты на единицу продукции составляют 0,2 с вероятностью 0,38. Пусть вероятность того, что BMA — это компания с низким уровнем затрат, составляет 0,4.
U12 (дополнительное упражнение).Вернитесь к истории с Океанией, где она закупает военное имущество у BMA (см. упражнение S11). Теперь проанализируйте ситуацию, в которой в BMA есть три возможных типа затрат: c 1, c 2и c 3, где c 3 > c 2 > c 1. BMA несет затраты c 1с вероятностью p 1, затраты c 2с вероятностью p 2и затраты c 3с вероятностью p 3, где p 1 + p 2 + p 3 = 1. Далее будем говорить, что компания BMA принадлежит к типу i , если ее затраты составляют c i при i = 1, 2, 3.
Вы предлагаете выбор из трех возможностей: «Мы выплатим вам сумму M i за поставку количества Q i при i = 1, 2, 3». Предположим, выбор более одного контракта обеспечивает равную прибыль, поэтому BMA типа i выберет контракт i . Для того чтобы удовлетворять условию участия, контракт i должен гарантировать компании BMA типа i неотрицательную прибыль.
a) Выведите формулу определения прибыли BMA типа i в случае, когда компания получает сумму M за поставку количества Q .
b) Сформулируйте условия ограничения участия для каждого типа BMA.
c) Укажите шесть ограничений совместимости стимулов. Другими словами, составьте выражение для каждого типа i , согласно которому прибыль, которую получит BMA в случае выбора контракта i , будет больше или равна прибыли, которую она получит при выборе двух других контрактов.
d) Составьте формулу определения ожидаемой чистой выгоды Океании B . Это и есть целевая функция (функция, которую необходимо максимизировать).
Теперь ваша задача — выбрать три значения Q i и три значения M i , обеспечивающие максимальную ожидаемую чистую выгоду с учетом ограничения совместимости стимулов (IC) и ограничения участия (PC).
e) Начните с трех ограничений: ограничение IC в отношении типа 2 подразумевает, что компания предпочтет контракт 2 контракту 3; ограничение IC в отношении типа 1 подразумевает, что компания предпочитает контракт 1 контракту 2; а также ограничение участия в отношении типа 3. Предположим, Q 1 > Q 2 > Q 3. Используйте эти ограничения для определения нижних пределов значений М 1, М 2и М 3, достижимых при соответствующих значениях c 1, c 2и c 3, а также Q 1, Q 2и Q 3. (Обратите внимание, что в выражении для нижней границы по каждому значению M может присутствовать два или более значения c и Q .)
f) Докажите, что три ограничения (два IC и одно PC), о которых идет речь в пункте е, связывающие в точке оптимума.
g) Теперь докажите, что, если три ограничения в пункте f связывающие, еще шесть ограничений (оставшиеся ограничения IC и два ограничения PC) удовлетворяются автоматически.
h) Подставьте соответствующие выражения вместо М i , выразив целевую функцию только через три Q i .
i) Запишите условия максимизации первого порядка и решите их относительно Q i . То есть возьмите три частные производные ∂ Q i /∂ B, приравняйте их к нулю и решите это уравнение относительно Q i .
j) Докажите, что указанное условие Q 1 > Q 2 > Q 3будет выполнено в точке оптимума, если
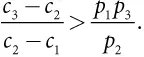
Часть IV. Применение теории игр в конкретных стратегических ситуациях
Глава 14. Балансирование на грани: Карибский кризис
* * *
В главе 1мы объяснили, что наш базовый подход основан на сочетании теории и анализа примеров из практики (то есть теоретические концепции разработаны исходя из особенностей конкретных ситуаций и примеров), а не на их изучении в чистом виде. Поэтому мы не учитывали те аспекты каждой ситуации, которые не имели прямого отношения к разрабатываемой концепции. Но теперь, изучив все теоретические идеи, вы можете применить более глубокий метод анализа, при котором подробная информация о конкретном случае полностью интегрирована в теоретико-игровой анализ, что обеспечивает более четкое понимание причин произошедшего. Такие теоретически обоснованные примеры из практики начали появляться в самых разных областях: бизнесе, политологии, истории экономики [249].
В данной главе мы рассмотрим пример из политической и военной истории, а именно балансирование на грани ядерной войны во время Карибского (Кубинского) кризиса 1962 года. Наш выбор обусловлен истинной драматичностью события, огромным объемом доступной информации и актуальностью одной из важнейших концепций теории игр.
Этот кризис, во время которого мир как никогда ранее оказался близок к развязыванию ядерной войны, действительно часто используют как классический пример балансирования на грани. Возможно, вы считаете, что риск ядерной войны исчез вместе с распадом СССР, поэтому наш пример не более чем экскурс в историю. Но гонка ядерных вооружений до сих пор продолжается во многих странах мира, а такие противники, как Индия и Пакистан или Иран и Израиль, могут найти применение урокам, извлеченным из Карибского кризиса. Для нас важнее то, что балансирование на грани применимо ко множеству других ситуаций, от политических и бизнес-переговоров до супружеских споров. Хотя ставки в таких играх ниже, чем в ядерной конфронтации между сверхдержавами, в них используются те же принципы построения стратегии.
В главе 9мы ввели концепцию балансирования на грани в качестве стратегического хода; вот краткий обзор того, о чем мы тогда говорили. Угроза — это правило ответа, которое влечет за собой определенные издержки как для игрока, который ее выдвигает, так и для игрока, на действия которого она должна повлиять. Тем не менее, если угроза достигает поставленной цели, это действие не выполняется. Следовательно, не существует явного верхнего предела издержек в связи с действием, составляющим суть угрозы. Однако риск ошибок (то есть риск того, что угроза может не достичь цели или соответствующее действие будет предпринято случайно) вынуждает стратега использовать минимальную угрозу, достигающую цели. Если более мелкую угрозу нельзя применить естественным образом, можно уменьшить масштаб крупной угрозы, поставив ее выполнение в зависимость от определенных условий. Вам необходимо заранее предпринять действие, создающее вероятность (но не неизбежность) того, что, если соперник проигнорирует вашу угрозу, это повлечет за собой последствия, пагубные для обеих сторон. Если бы действительно возникла потребность реализовать угрозу, вы бы не стали этого делать при наличии полной свободы выбора. Следовательно, вы заранее должны позаботиться о том, чтобы ситуация в какой-то мере вышла из-под вашего контроля. Балансирование на грани — и есть создание и приведение в действие такой вероятностной угрозы, включающей в себя элемент намеренной потери контроля.
Читать дальшеИнтервал:
Закладка:










