Авинаш Диксит - Стратегические игры

Рис. 4.14.Отсутствие равновесия в чистых стратегиях

Правила решения игр с одновременными ходами говорят нам о том, что сначала следует попытаться найти доминирующие или доминируемые стратегии, а затем использовать анализ наилучшего ответа для поиска равновесия Нэша. Это полезное упражнение позволяет убедиться, что в данной игре нет доминирующих стратегий. Выполнив анализ наилучших ответов, мы приходим к выводу, что лучший ответ Эверт на стратегию ПЛ — стратегия ПД, а на стратегию ПД — стратегия ПЛ. Напротив, наилучший ответ Навратиловой на стратегию ПЛ — стратегия ПЛ, а на стратегию ПД — стратегия ПД. Ни в одной ячейке таблицы выигрышей равновесия Нэша нет, поскольку каждая теннисистка упорно пытается изменить свою стратегию. Например, начав с верхней левой ячейки таблицы, мы обнаружим, что Эверт предпочитает перейти от стратегии ПЛ к стратегии ПД, увеличив свой выигрыш с 50 до 90 процентов. Однако в левой нижней ячейке таблицы мы видим, что Навратилова считает разумным переключиться со стратегии ПЛ на ПД, увеличив свой выигрыш с 10 до 80 процентов. Как вы можете убедиться сами, аналогичным образом Эверт стремится изменить стратегии в нижней левой ячейке, а Навратилова — в верхней правой. В каждой ячейке таблицы одна участница неизменно старается изменить игру, поэтому мы можем бесконечно перемещаться в таблице по кругу в поисках равновесия.

Отсутствие равновесия Нэша в этой и других подобных играх содержит один значимый сигнал: в играх такого типа важно не то, что игроки должны сделать, а то, чего они не должны делать . В частности, каждая участница игры не должна постоянно или систематически выбирать один и тот же удар, оказываясь в такой ситуации. Если любая из теннисисток будет придерживаться определенной линии поведения, другая может воспользоваться этим. (Например, если бы Эверт постоянно делала обводящий удар по диагонали, Навратилова бы знала, что ей каждый раз необходимо прикрывать соответствующую сторону корта, и тем самым снизила бы шансы Эверт на успешное выполнение удара по диагонали.) Самое разумное, что могут сделать участницы игры, — действовать несколько бессистемно, рассчитывая на то, что элемент неожиданности поможет победить соперницу. Асимметричный подход подразумевает выбор каждой стратегии в определенном количестве случаев. (Эверт следует использовать свой более слабый удар достаточно часто, чтобы Навратилова не могла предугадать, какой удар будет направлен в ее сторону. Однако она не должна использовать удары двух типов по установленной схеме, поскольку это также приведет к потере элемента неожиданности.) Подход, при котором игроки выбирают действия случайным образом, известный как смешивание стратегий, подробно рассматривается в главе 7. Игра, представленная на рис. 4.14, может не иметь равновесия в чистых стратегиях, но ее все же можно решить посредством поиска равновесия в смешанных стратегиях, что мы и сделаем в разделе 1 главы 7.

Участники игр с одновременными ходами выбирают стратегии, не зная о выборе других игроков. Такие игры можно изобразить в виде таблицы игры , в ячейках которой отображены выигрыши каждого игрока, а ее размерность равна количеству игроков. Игры с нулевой суммой с двумя участниками можно представить в сокращенном виде, отобразив в каждой ячейке таблицы игры только выигрыши одного игрока.

Равновесие Нэша — концепция, используемая для решения игр с одновременными ходами. Такое равновесие состоит из совокупности стратегий (по одной на каждого игрока), где каждый игрок выбрал свой лучший ответ на выбор другого игрока. Кроме того, равновесие Нэша можно трактовать как набор стратегий, при котором у каждого игрока есть правильные убеждения относительно стратегий других игроков, а определенные стратегии являются лучшими для каждого игрока с учетом этих убеждений. Равновесия Нэша можно найти посредством поиска доминирующих стратегий, последовательного исключения доминируемых стратегий или анализа наилучших ответов .

Существует масса классов игр с одновременными ходами. Игра «дилемма заключенных» встречается во многих контекстах. В координационных играх, таких как игра в доверие, игра в труса и битва полов , — множество равновесий, и решение этих игр требует от их участников координации действий. Если в игре отсутствует равновесие в чистых стратегиях , мы должны искать его в смешанных стратегиях , анализ которых представлен в главе 7.

Анализ наилучших ответов

Битва полов

Дилемма заключенных

Доминируемая стратегия

Доминирующая стратегия

Игра в доверие

Игра в труса

Игра с чистой координацией

Итеративное исключение доминируемых стратегий

Координационная игра

Матрица игры

Наилучший ответ

Нормальная форма

Последовательное исключение доминируемых стратегий

Равновесие Нэша

Разрешимость по доминированию

Смешанная стратегия

Стратегическая форма

Сходимость ожиданий

Таблица выигрыша

Таблица игры

Убеждение

Фокальная точка

Чистая стратегия

S1.Найдите все равновесия Нэша в чистых стратегиях для представленных ниже игр. Сначала проверьте таблицу игры на наличие доминирующих стратегий. Если таковых нет, решите игру посредством итеративного исключения доминируемых стратегий. Объясните логику своих рассуждений.

a)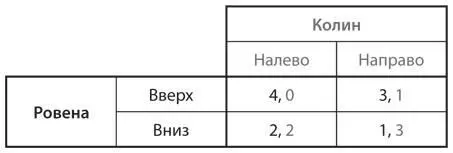

b)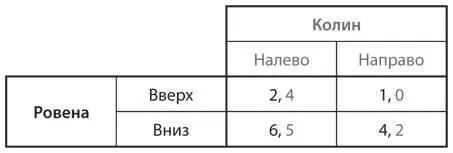

c)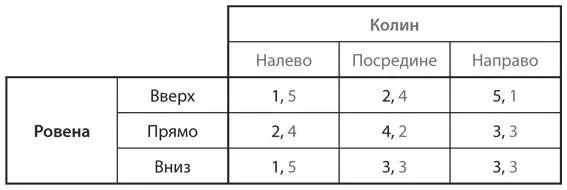

d)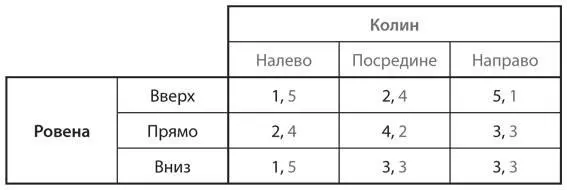

S2.Для каждой из четырех игр, представленных в упражнении S1, определите, это игра с нулевой или с ненулевой суммой. Объясните логику своих рассуждений.

S3.Метод минимакса — еще один значимый способ решения игр с нулевой суммой, разработанный задолго до того, как Нэш сформулировал концепцию равновесия в играх с ненулевой суммой. Для того чтобы его применить, необходимо исходить из предположения, что независимо от того, какую стратегию выберет игрок, его соперник сделает такой выбор, который обеспечит этому игроку худший выигрыш от данной стратегии. В случае каждой игры с нулевой суммой, найденной в упражнении S2, используйте метод минимакса для поиска равновесных стратегий игры, выполнив следующие действия: