Виталий Сигорский - Математический аппарат инженера

- 565 -

Ясно, что последовательностные схемы должны обладать способностью сохранять предыдущее состояние до следующего такта, в связи с чем их называют также автоматами с памятью или последовательностными машинами. В качестве памяти могут использоваться элементы задержки, на выходах которых повторяются входные воздействия со сдвигом во времени на интервал между тактами D t . Широко применяются также различные запоминающие элементы, например, триггеры, способные сохранять состояния на выходах до тех пор, пока оно не изменяется в результате воздействия на их входы.

3. Типы конечных автоматов.В технике с понятием автомата обычно связывается некоторое устройство, способное выполнять определенные функции без вмешательства человека или с его ограниченным участием. Однако такое понимание является слишком узким. В широком смысле конечный автомат - это математическая модель, отображающая физические или абстрактные явления самой разнообразной природы. Такая модель успешно используется как в технике (проектирование электронных вычислительных машин, систем управления и связи), так и в других областях - психологии и физиологии (исследование деятельности нервной системы человека и простейших видов поведения животных), лингвистике (анализ синтаксиса русского, английского или других языков, расшифровка древних рукописей), теории и практике административного управления и т.п. Универсальность теории автоматов позволяет рассматривать с единой точки зрения различные объекты, устанавливать связи и аналогии между ними, переносить результаты из одной области в другую.

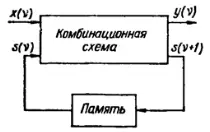
Рис. 235. Блок-схема конечного автомата.

Конечный автомат М определяется как система с конечным входным алфавитом Х = { ξ 1, ξ 2, ... , ξ p}, конечным выходным алфавитом Y = { v 1, v 2, …, v q}, конечным множеством состояний S = {σ 1, σ 2, ..., σ i}, и двумя характеристическими функциями:

s(ν + 1) = δ (x(ν), s(ν));

у (ν) = λ ( х (ν) , s (ν)),

называемыми соответственно функцией переходов и функцией выходов. Общая блок-схема конечного автомата (рис. 235) может быть представлена в виде комбинационной схемы, реализующей характеристические функции δ и λ, и памяти, сохраняющей на один такт предыдущее состояние автомата.

В определении автомата участвует три конечных множества X, Y, S и две функции δ и λ, задающие некоторые отношения между

- 566 -

элементами этих множеств. Следовательно, конечный автомат можно обозначить упорядоченной пятеркой М = (X, Y, S, δ, λ). Мощности множеств X , Y, S равны соответственно:

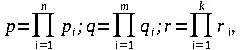
где p i, q i, r i - количество символов в алфавитах входной переменной x i , выходной переменной y i и переменной состояния s i . При двоичном структурном алфавите р = 2 n , q = 2 m и r = 2 k . Если желают подчеркнуть мощности множеств X , Y и S , на которых определен конечный автомат, то его называют (р, q, r )-автоматом.

Характеристические функции δ и λ можно рассматривать как некоторые отображения множества X × S или его подмножества D ⊂ X × S соответственно на множества S и Y . Если δ : X × X → S и λ : X × S → Y, автомат называется полным; если только δ : X × S → S, автомат называют полным по переходам. В случае, когда функции δ и λ определены не для всех наборов из множества X × S, автомат называют неполным или частично определенным.

Приведенное в начале этого параграфа определение связывают обычно с автоматом первого рода, называемым также автоматом Мили. Если выходные переменные являются функцией только состояния, то имеем автомат второго рода или автомат Мура.

Между автоматами этих двух типов имеется взаимная связь и один из них может быть преобразован в другой. Положив в характеристических функциях автомата Мили s' ( ν ) = (x( ν ), s( ν )), получим у ( ν ) = λ ' ( s' ( ν )) и s' ( ν + 1) = (x( ν + 1), s( ν + 1)) = (x( ν + 1); δ (x( ν ), s( ν ))) = δ (x( ν + 1), s' ( ν )), т. е. приходим к автомату Мура. Обратный переход осуществляется подстановкой s( ν ) = s' ( ν - 1), в результате чего получаем у ( ν ) = λ ' ( s' ( ν )) = λ ' ( δ (x( ν ), s' ( ν - 1))) = λ (x( ν ), s( ν )), а также s( ν + 1) = s' ( ν ) = δ (x( ν ), s' ( ν - 1)) = δ (x( ν ), s( ν )).

Для комбинационных схем функция перехода не имеет смысла, а функция выходов вырождается к виду y ( ν ) = λ (x( ν )). Их называют автоматами без памяти или тривиальными автоматами.

4. Представления конечных автоматов.Автомат может быть задан различными способами, например, путем словесного описания его функционирования или перечислением элементов множеств X , Y , S , с указанием отношений между ними. При анализе и синтезе конечных автоматов используются стандартные формы представления: таблицы, графы и матрицы. Элементы множеств X , Y , S удобно пронумеровать порядковыми числами, начиная с нуля, например: Х = {0, 1, 2, 3}, Y = {0, 1} и S = {0, 1, 2, 3}. Тогда характеристические функции δ и λ можно представить двумя

- 567 -

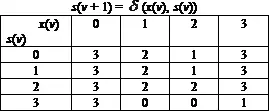
таблицами, строки которых соответствуют состояниям, а столбцы - входам. Первая таблица, называемая таблицей переходов, соответствует функции s( ν + 1) = δ (x( ν ), s( ν )), и ее клетки заполняются номерами состояний s( ν + 1), в которые переходит автомат при

воздействии х ( ν ) , и состоянию s( ν ) в данный тактовый момент. Вторая таблица, называемая таблицей выходов, соответствует функции у ( ν ) = λ (x( ν ), s( ν )), и ее клетки заполняются номерами выходов y ( ν ) в данный тактовый момент, которые соответствуют воздействию x( ν ) и состоянию s( ν ) в тот же момент. Например, для заданных множеств X , Y, S такие таблицы могут иметь вид:

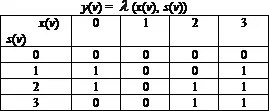Обе таблицы можно объединить в общую таблицу переходов, если условиться записывать в клетках пары чисел (номер следующего состояния в числителе и номер выхода в знаменателе), т.е.

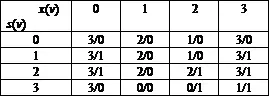
Граф автомата строится таким образом, что его вершины соответствуют состояниям, а направленные дуги обозначаются как дизъюнкции входов, под воздействием которых совершается переход из одного состояния в другое по направлению дуги. В знаменателях записываются номера выходов, соответствующие этим переходам.