Виталий Сигорский - Математический аппарат инженера

Объединение эквивалентных состояний в классы эквивалентности осуществляется весьма просто. Если σ i ~ σ j и σ j ~ σ k, то на основе свойства транзитивности следует, что σ i ~ σ k , и, значит, пары { σ i , σ j} и { σ j , σ k} входят в общий для них класс эквивалентности. Но для выявления всех пар эквивалентных состояний требуется более громоздкая процедура, так как множество таких пар не исчерпывается явно эквивалентными состояниями и не всегда может быть полностью обнаружено и объединено способом, изложенным ранее.

Для эквивалентного разбиения множества S состояний автомата предложен ряд способов. Один из них основан на последовательном рассмотрении всевозможных пар состояний и исключении тех из них, которые не являются эквивалентными. При этом пары одинаковых состояний { σ i , σ i} , являющиеся в силу свойства рефлективности заведомо эквивалентными { σ i ~σ i} , не рассматриваются. Процедура эквивалентного разбиения осуществляется по таблице пар состояний, которая получается на основе общей таблицы переходов автомата. Так как явно различимые пары состояний (для таких состояний строки в таблице выходов различные) не могут быть эквивалентными, то они в таблицу пар не включаются. Для каждой пары отводится строка, для каждого входа – столбец, ав клетках на основании таблицы переходов указывается пара состояний, в которые переходит автомат из данной пары состояний при данном входном воздействии (порядок записи состояний в каждой паре безразличен). Исключаемые пары отмечаются каким-либо способом (набираются жирным шрифтом, подчеркиваются или снабжаются меткой). Далее приведены общая таблица переходов (табл. 10) и полученная из нее таблица пар состояний некоторого автомата.

- 575 -

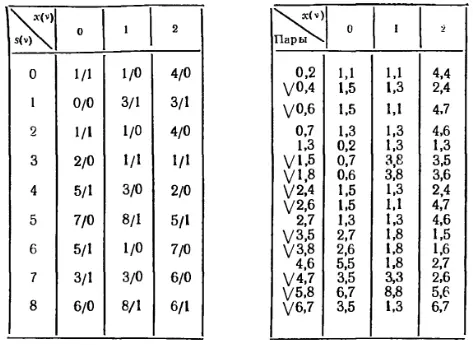
Так как одинаковые строки таблицы выходов соответствуют множествам состояний {0, 2, 4, 6, 7} и {1, 3, 5, 8}, то в первом столбце таблицы пар указаны только попарные комбинации таких состояний, которые входят в одно и то же множество, т. е. не являются явно различимыми.

Исключение пар основано на следующем положении: если состояния σ i и σ j эквивалентны, то эквивалентными являются и состояния, в которые автомат переходит под любым входным воздействием. Это значит, что на первом шаге необходимо отметить те пары, которые переходят в пары, состоящие из различных состояний и отсутствующие в первой графе таблицы. Так как обозначенные пары не могут быть эквивалентными, то на следующем шаге отмечаются все те пары, которые переходят в пары, отмеченные на предыдущем шаге и т. д. Процесс заканчивается тогда, когда среди неотмеченных пар уже нет таких, которые можно отметить в соответствии с изложенным правилом. После этого неотмеченные пары и представляют собой попарно эквивалентные состояния.

В приведенном примере на первом шаге отмечаются пары {1, 8}, {3, 8} и {5, 8}, на втором – {1, 5} и {3, 5}, на третьем – {0, 4}, {0, 6}, {2, 4}, {2, 6}, {4, 7} и {6, 7}. Эквивалентными являются неотмеченные пары {0, 2}, {0, 7}, {1, 3}, {2, 7} и {4, 6}, образующие классы эквивалентности S 0= {0, 2, 7}, S 1= { 1, 3} и S 2= { 4, 6}. Кроме того, не вошедшие в эти множества состояния 5 и 8 образуют классы эквивалентности S 3= {5} и S 4= {8}. Обозначив представителей полученных пяти классов соответственно числами от 0 до

- 576 -

4, получим для рассматриваемого автомата минимальную форму с пятью состояниями и общей таблицей переходов:

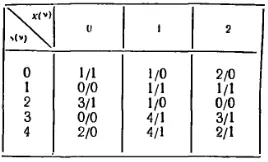
Следует отметить, что автомат, все состояния которого эквивалентны, сводится к автомату с одним состоянием, т. е. представляет собой по существу комбинационную схему. Автомат, среди состояний которого нет эквивалентных, является несократимым.

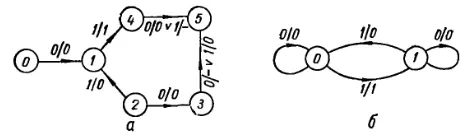
Рис. 241. Граф неполного автомата (а) и его минимальная форма (б).

Если М' – минимальная форма автомата М , то она единственна и несократима.

9. Неполные автоматы. В практике встречаются случаи, когда не каждый символ из входного алфавита может быть подан на автомат, находящийся в определенном состоянии (ограничения на входе), или его выходы при некоторых входных воздействиях не представляют интереса (неопределенность выходов). Тогда приходится иметь дело с неполными автоматами, общая таблица переходов которых содержит прочерки вместо состояний и выходов для запрещенных входов, а также вместо неопределенных выходов.

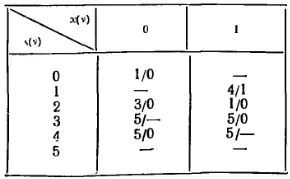
Например, таблица для неполного автомата, граф которой изображен на рис. 241, a, имеет следующий вид:

- 577 -

Здесь вход 0 в состояниях 1 и 5, а также вход 1 в состояниях 0 и 5 являются запрещенными. Кроме того, в состоянии 3 при воздействии 0 и в состоянии 4 при воздействии 1 выходы не определены.

Входная последовательность называется допустимой для автомата в состоянии s i , если она не нарушает ограничений на входе ни в каком состоянии автомата М и порождаемый ею выход определен на заключительном такте. На других тактах входной последовательности выходы могут быть и не определены, но последовательность состояний обязательно должна существовать. Например, для приведенного автомата в состоянии 0 допустимая входная последовательность {0, 1,0} порождает последовательность состояний {1, 4, 5} и заключительный выход 0. В то жевремя последовательность {0, 1, 1} не допустима, так как заключительный выход не определен.

Число состояний неполного автомата иногда можно сократить изложенными в предыдущих разделах методами, произвольно интерпретируя прочерки в его таблице и рассматривая его как полный автомат. Однако такой путь не гарантирует получения минимальной формы.

Сокращенная форма неполного автомата М – это такой автомат М', который по отношению к допустимым для М входным последовательностям ведет себя на выходах так же, как и исходный автомат М, но имеет меньшее число состояний. Автомат М' квазиэквивалентен автомату М. Отношениеквазиэквивалентности рефлексивно и транзитивно, но не симметрично, т. е обладает всеми свойствами отношения включения. Поэтому говорят также, что М' включает М и записывают М ⊂М'. При этом из М ⊂М' вовсе не следует М' ⊂М, что иногда выражают словами: М' делает столько же и, быть может, больше, чем М.

10. Минимизация неполных автоматов. Эта задача сводится к поиску квазиэквивалентного автомата, который имеет наименьшее число состояний, и решается следующим образом.