Рафаель Роузен - Математика для гиков
- Название:Математика для гиков
- Автор:
- Жанр:
- Издательство:Литагент АСТ
- Год:2016
- Город:Москва
- ISBN:978-5-17-096852-7
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Рафаель Роузен - Математика для гиков краткое содержание
После прочтения вы сможете использовать в разговоре такие термины как классификация Дьюи, Числа Фибоначчи, равновесие Нэша, парадокс Монти Холла, теория хаоса, подготовитесь к тексту Тьюринга, узнаете, как фильм получает Оскар, и что это за эффект бразильского ореха.
Математика для гиков - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
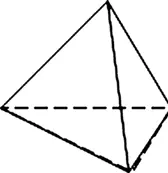
Каждое платоново тело содержит так называемый двугранный угол, который является внутренним углом между двумя гранями. Так как каждая грань платонова тела одинакова, значит, все двугранные углы этого тела тоже будут равными. Например, в кубе двугранный угол равен 90 градусам, как и угол при вершине. Но в тетраэдре двугранный угол равен 70,6 градуса, а угол при вершине – 60 градусам. Чем больше двугранный угол, тем больше тело будет напоминать шар.
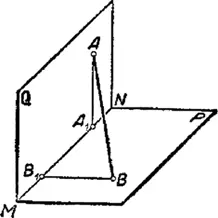
1.21. Почему на мячике для гольфа есть впадинки?
Математические понятия: физика, геометрия
Когда вы смотрите, как Тайгер Вудс делает первый удар на открытом чемпионате США по гольфу, вы можете не представлять, что за этим моментом скрывается математика, которая помогает его мячу лететь сквозь воздух. Но это правда, а все благодаря геометрии впадинок на мяче.
Сотни лет назад мячи для гольфа делали из дерева или резины, а поверхность их была абсолютно гладкая. Согласно легенде в мире гольфа, когда гольфисты вновь и вновь использовали один мяч, они заметили, что старые, неровные мячи летели дальше, чем новые, гладкие. Позже ученые поняли, что ямки или впадинки позволяют воздуху вокруг мяча оставаться ближе к изогнутой форме мяча, уменьшая турбулентность в воздухе за мячом, которая и вызывает торможение. Традиционно ямки имеют форму круга, но недавно их стали делать в форме шестиугольников. Производитель Callaway утверждает, что шестиугольные ямки покрывают больше поверхности мяча, следовательно, на нем меньше плоской поверхности между каждой ямкой и, естественно, меньше торможения.
Мячи для гольфа бывают разных размеров, но в основном имеют 300–500 ямок. Обычный мяч для гольфа имеет 336 ямок.
1.22. Гаусс и пицца
Математическое понятие: фигуры
Проведите эксперимент: возьмите газету и оберните ей арбуз, словно хотите подарить его другу на день рождения. Что же получается? Неважно, как усердно вы стараетесь, но на нем всегда будут складки и загибы, которые будут торчать в разные стороны; бумага никогда не будет лежать ровно на поверхности арбуза. (Чтобы бумага повторила форму арбуза, вам необходимо взять ножницы и разрезать ее на части, но даже в этом случае вам скорее всего, придется время от времени приглаживать складки.) В действительности невозможно сложить такую ровную поверхность, как лист бумаги, в форму шара, не разрезая и не сгибая его.
Обратное действие будет таким же трудным. Очистите грейпфрут так, чтобы у вас остался один кусок в форме шара, и попытайтесь его разгладить. Шкурка неизбежно порвется. Вы не сможете ее полностью разгладить, если не порежете или не порвете ее. Но почему превращение плоской поверхности в круглую или круглой в плоскую такое трудное? Что мешает плоской и круглой поверхностям спокойно преобразовываться одна в другую?
Ответ скрывается в куске пиццы и в работах Карла Фридриха Гаусса, немецкого математика, который родился в 1777 году и умер в 1855 году. (Гаусс занимает особое место в истории математики. Его считают одним из величайших математиков со времен Древней Греции и обычно называют Принцем Математики. Не забывайте, что он был учителем Августа Фердинанда Мебиуса – см. главу 1.7.) Гаусс доказал теорему об искривлении поверхности, которая известна как theorem egregium (от лат. – «выдающаяся теорема»).
Чтобы понять теорему Гаусса, представьте человека, которого уменьшили до одного дюйма и поместили на поверхность цилиндра. Если человек начинает идти, он может найти множество маршрутов, которым он может следовать. Например, он может пройти вдоль верхушки цилиндра по прямой линии. Или он может пройти вдоль изогнутой части цилиндра по кругу, пока не вернется в отправную точку. (Нам придется представить, что этот человек надел уж очень липкие ботинки.) Он также мог бы идти по спирали, кружась вокруг цилиндра и одновременно продвигаясь вдоль его длины. Теорема Гаусса гласит, что можно измерить кривизну этого цилиндра, используя все эти маршруты, их нужно умножить друг на друга, и получится значение. Плоская поверхность имеет нулевую кривизну – в конце концов, она плоская, – а криволинейная траектория имеет положительную кривизну. (Вогнутая кривая – которая выгнута внутрь – будет иметь отрицательную кривизну.) Когда вы умножаете кривизны, то в итоге умножаете положительное значение на ноль, в результате чего получается ноль (так как любое число, умноженное на ноль, дает ноль). Получается, что цилиндр имеет нулевую гауссовскую кривизну.
В теореме Гаусса также говорится о поверхности фигуры. Утверждается, что вы можете сгибать и растягивать поверхность и она будет иметь ту же гауссовскую кривизну, что и изначально, до тех пор, пока вы не нарушите ее целостность. Поэтому неважно, как сильно вы будете мять или деформировать цилиндр, гауссовская кривизна от этого не изменится.
Это приводит нас к пицце. Если вы когда-нибудь пытались держать большой кусок пиццы ровно в руке, особенно если на этом куске много расплавленного сыра и пеперони, то вы знаете, что конец пиццы всегда падает и вам становится трудно его есть. С другой стороны, если вы сложите кусок продольно, то конец вовсе не падает, а смотрит прямо, а начинка остается там, где ей и место. В чем же дело? Итак, если вы посчитаете кривизну не согнутого куска пиццы, то получите ноль. (Любые возможные траектории, по которым может пройти однодюймовый человек на поверхности куска являются плоскими.) А это значит, что вы можете сколько угодно двигать или сгибать этот кусок, но его кривизна будет все равно равна нулю.
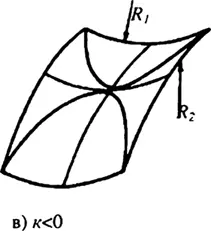
А теперь посмотрите на кусок пиццы, конец которого смотрит вниз. Траектория от корочки до конца будет изогнутой, а траектория от одной стороны до другой – прямой. Теперь если мы сложим кусок, то траектория от одной стороны до другой будет кривой, а от корочки до конца – прямой.
Что же все это значит? Неважно, как согнут кусок, одна возможная траектория должна быть прямой (так как плоская кривая имеет нулевую гауссовскую кривизну, и нам нужен ноль в расчетах, чтобы получить в результате ноль). Если траектория между сторонами плоская, то траектория от начала до конца будет кривой. Если траектория от начала до конца плоская, то траектория между сторонами будет кривой.
Читать дальшеИнтервал:
Закладка:










