Рафаель Роузен - Математика для гиков
- Название:Математика для гиков
- Автор:
- Жанр:
- Издательство:Литагент АСТ
- Год:2016
- Город:Москва
- ISBN:978-5-17-096852-7
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Рафаель Роузен - Математика для гиков краткое содержание
После прочтения вы сможете использовать в разговоре такие термины как классификация Дьюи, Числа Фибоначчи, равновесие Нэша, парадокс Монти Холла, теория хаоса, подготовитесь к тексту Тьюринга, узнаете, как фильм получает Оскар, и что это за эффект бразильского ореха.
Математика для гиков - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Используя технологии, разработанные в 1950-х для улучшения морских гидролокаторов, математик Скотт Рикард создал музыкальное произведение без повторов, но это не значит, что оно было абсолютно беспорядочно, и назвал его «самой неприятной музыкой в мире».
3.4. Игра Го
Математическое понятие: комбинаторика
Многие игры имеют математическое подспорье, но, пожалуй, одна из них выделяется больше всех – это игра Го. Считается, что она была изобретена в Китае примерно 4000 лет назад. Эта игра особенно популярна в Китае, Японии и Корее и постепенно завоевывает западное сознание. (Например, американская ассоциация Го была создана лишь в 1935 году.) Правила игры просты: у одного игрока есть коллекция черных камней, а у другого – белых. Доска, которая обычно сделана из дерева, разделена на 19 × 19 линий, то есть сетка состоит из 19 полос и 19 столбиков. Игроки ставят камни на пересечении линий сетки с целью захвата и защиты территории. Вы можете захватить вражеский камень, окружив его своими камнями. Когда камень окружен, его убирают с доски.
Го практически утопает в математике. Например, посчитайте количество допустимых позиций: чуть больше, чем 2 × 10 170, а когда вы узнаете, что число атомов в известной нам Вселенной равно примерно 10 84, то эта цифра покажется еще невероятнее. Большие числа появляются также, когда вы сравниваете Го с шахматами. Когда в шахматы играет компьютерная программа, она может проанализировать последствия каждого хода, вплоть до семи ходов вперед. Но если компьютер применил бы эту технику к Го, то у него бы быстро случилась перегрузка. В шахматах компьютер может прорабатывать до 60 миллиардов возможностей во время каждого хода. Однако, чтобы думать на семь ходов вперед в Го, компьютеру придется просмотреть 10 000 триллионов возможностей.
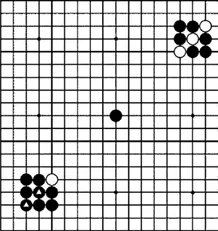
Эта игра также помогла появиться совершенно новому классу чисел. В 1970 году математик Джон Конвей из Кембриджского университета изучал игру Го, в которую играли два мастера, и в результате пришел к идее сюрреальных чисел. Вы можете рассматривать сюрреальные числа как наборы инструкций, чтобы найти определенные числа на числовой прямой с помощью серии движений вверх и вниз. Все действительные числа – которые состоят из целых чисел, дробей, положительных, отрицательных и иррациональных чисел – считаются сюрреальными, но некоторые сюрреальные числа не являются действительными. В сущности, сюрреальные числа – это новый набор чисел (как рациональные или целые числа), которые вы можете найти на числовой прямой с помощью серии ходов: вниз, вверх, влево, вправо. Одним особенно большим сюрреальным числом является омега, это число на числовой прямой, когда вы следуете вправо бесконечное количество времени. (Омега – это наименьшее сюрреальное число, которое больше, чем любое действительное число.) В любом случае, толчком для этого открытия стала игра Го, и по сей день она приносит математическое удовольствие миллионам людей по всему миру.
Отелло – это игра, чем-то напоминающая Го, ее изобрели в 1880-х два англичанина, изначально она называлась Реверси, хотя игры имеют достаточные различия. В обеих играх игроки окружают камни противника, в Отелло окруженные камни, черные с одной стороны и белые с другой, переворачиваются. В Го окруженные камни остаются того же цвета. Кроме того, доска в Отелло имеет разлиновку 8 × 8, что куда меньше, чем 19×19 в Го.
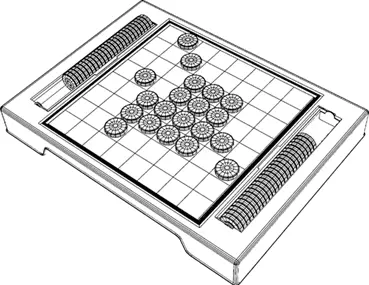
3.5. Шахматная доска и пшеница
Математическое понятие: геометрическая прогрессия
Существует история, согласно которой визирь при дворе короля Ширхама в Индии Сисса Бен Дахир изобрел игру в шахматы. Довольный изобретением Дахира король Ширхам предложил ему выбрать в качестве дара то, что он захочет. Сисса Бен Дахир попросил, казалось бы, безобидный дар: одно зерно пшеницы за первый квадрат шахматной доски, два за второй, четыре за третий и так далее, каждый последующий квадрат получал в два раза больше зерна, чем предыдущий. Мы можем представить этот процесс в виде суммирования: 2 0+ 2 1+ 2 2+ 2 3+… 2 63. (Мы остановились на 63, так как, хоть и на доске 64 квадрата, степень первой 2 равна 0, а не 1.) Такое суммирование, где число остается неизменным, а степень растет с каждым шагом прогрессии, называется геометрической прогрессией. И хоть и кажется, что сумма будет не такой уж большой, она на самом деле будет огромной. На деле это число будет равно числу шагов, которые необходимы, чтобы решить задачу Ханойской башни, то есть 18 446 744 073 709 551 615 (см. главу 3.4). Если предположить, что в тонне пшеницы примерно 100 миллионов зерен, Сисса Бен Дахир попросил примерно 200 миллиардов тонн пшеницы. Действительно ошеломительное количество.
Самая впечатляющая коллекция шахмат в мире известна как шахматы с острова Льюис. Она состоит из 93 фигур XII века, которые были обнаружены в 1831 году на шотландском острове Льюис (Внешние Гебриды). Они изготовлены из моржовых костей и зубов китов, и кажется, что они имеют скандинавские корни: ладьи выполнены в форме солдат, кусающих свои щиты, как это делали берсерки.
3.6. Ханойская башня
Математические понятия: рекурсия, геометрическая прогрессия
Иногда простые правила могут привести к удивительно большим числам. Представьте Ханойскую башню, игрушку, состоящую из трех стержней, установленных вертикально на устойчивой базе, и стопки деревянных колец – у каждого отверстие в центре, – нанизанной на один стержень. Каждый диск разного размера, и они сложены так, что самый маленький диск лежит сверху и, по мере возрастания, самый большой лежит снизу. Целью игры является переместить стопку дисков на другой стержень так, чтобы диски лежали в том же порядке, но вы можете передвигать только один диск за раз, и нельзя класть больший диск на меньший.
Шаги, необходимые для достижения цели, являются примером рекурсии. Передвижение первого диска требует одного хода, но каждый последующий диск требует в два раза больше ходов, чем предыдущий. Если дисков много, то количество ходов для решения головоломки непостижимо велико. Например, существует легенда о Ханойской башне. Согласно этой легенде, в Индии есть Ханойская башня с тремя алмазными иглами, и на одной из них находятся 64 золотых диска, каждый меньше чем тот, что под ним. Монахи Брахмы следят за дисками, и постоянно один из монахов переставляет диски на другую иглу, согласно тем простым правилам, которые были упомянуты ранее.
Читать дальшеИнтервал:
Закладка:










