Рафаель Роузен - Математика для гиков
- Название:Математика для гиков
- Автор:
- Жанр:
- Издательство:Литагент АСТ
- Год:2016
- Город:Москва
- ISBN:978-5-17-096852-7
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Рафаель Роузен - Математика для гиков краткое содержание
После прочтения вы сможете использовать в разговоре такие термины как классификация Дьюи, Числа Фибоначчи, равновесие Нэша, парадокс Монти Холла, теория хаоса, подготовитесь к тексту Тьюринга, узнаете, как фильм получает Оскар, и что это за эффект бразильского ореха.
Математика для гиков - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Золотое сечение можно также найти в фигуре под названием «золотой прямоугольник». Соотношение ширины и длины этого прямоугольника равно 1:1.618 (продлен до бесконечности). Кроме того, если вы нарисуете внутри прямоугольника квадрат, то оставшийся прямоугольник имеет те же пропорции, что и изначальный прямоугольник! Другими словами, соотношение меньшей ширины и меньшей длины (b: a) равно соотношению большей ширины и большей длины (a: a + b).
Архитекторы и художники использовали золотое сечение в своих работах в течение тысячелетий, с тех пор, как человечество решило, что эта пропорция особенно приятна для глаза. Вот несколько примеров:
• Воображаемый прямоугольник, начерченный вокруг передней части Парфенона в Афинах, имеет эти пропорции.
• Великая пирамида в Гизе, одно из оригинальных семи чудес света, также включает в себя золотое сечение. Соотношение длины одной из сторон пирамиды – наклонной – и половины длины основания равно 1,61804.
• Если проанализировать «Тайную вечерю» да Винчи и «Сотворение Адама» Микеланджело на потолке Сикстинской капеллы, вы заметите, что обе композиции основываются на золотом сечении.
В любом музее будет полно примеров 1:1,618, как и в любом городе. Эти цифры вас окружают.
Многие верят, что люди использовали золотое сечение в искусстве и архитектуре на протяжении тысячелетий. С другой стороны, некоторые математики считают, что нет доказательств таким утверждениям и заявления, что в создании Великих пирамид, Парфенона или даже в работах Леонардо да Винчи использовано золотое сечение – всего лишь миф.

4.12. Золотое сечение в твоей ДНК
Математические понятия: золотое сечение, последовательность Фибоначчи
Помимо появления в мире искусства, золотое сечение еще можно найти повсюду в природе. На самом деле золотое сечение является частью нас самих. Оно встроено в каждую молекулу ДНК в каждой клетке нашего организма. (ДНК, или дезоксирибонуклеиновая кислота, кодирует информацию для создания белков, что, в свою очередь, помогает создавать структуру органов тела и тканей и регулировать их функции. Гормоны и ферменты являются белками, как и актин, который помогает мышцам сокращаться. Актин также является частью внешнего скелета клетки, который придает клетке форму.) Структура молекулы ДНК была расшифрована Джеймсом Уотсоном и Фрэнсисом Криком в 1953 году, которые и показали двойную спираль. Каждый полный поворот спирали состоит из 34 ангстрем в длину и 21 ангстрема в ширину – ангстрем составляет 100-миллионную долю сантиметра – и соотношение этих двух чисел равно 1:1,6190, что очень близко к золотому сечению 1:1,618.
Эти числа, 34 и 21, особенные еще по одной причине: они появляются в последовательности Фибоначчи, ряде чисел, который был открыт Леонардо Фибоначчи в XIII веке (см. главу 4.5). Каждое число в последовательности получается в результате сложения двух предыдущих чисел. И когда вы сравниваете два рядом стоящих числа в последовательности, соотношение между ними примерно равно золотому сечению. Кроме того, чем выше числа в последовательности, тем больше это значение будет приближено к золотому сечению. Таким образом, соотношение 5 и 8, стоящих почти в самом начале, равно 1:1,6, а соотношение 377 и 610 равно 1:1,61803714. Этот результат соответствует золотому сечению вплоть до пятой цифры после запятой.
Греческая буква Фи ( φ )была впервые использована для обозначения золотого сечения в 1909 году американским математиком Марком Барром в честь Фидия, древнегреческого скульптора; многие люди считали, что он использовал золотое сечение в своих работах.
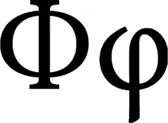
4.13. Эпитрохоиды с помощью детских игрушек
Математическое понятие: фигуры
Одни из самых интересных математических фигур появляются в игрушках. Например, вы можете узнать, что такое эпитрохоиды, а также гипотрохоиды и рулетты, если повозитесь со спирографом. Если у вас когда-нибудь была возможность поиграть с этой игрушкой, то вы знаете, что она обычно состоит из двух полых внутри пластиковых кругов, с зубчатым внутренним или внешним краем. В комплекте также есть несколько пластиковых колес с зубчатым внешним краем и несколькими отверстиями внутри колеса, куда вставляется кончик ручки. Вы кладете один из пластиковых кругов на лист бумаги с картонной подложкой, затем выбираете колесо, вставляете ручку в отверстие и кладете колесо к внешнему или внутреннему зубчатому краю круга. Потом вы начинаете двигать колесо ручкой по кругу, тем самым на бумаге остаются замысловатые геометрические узоры.
Вот где появляются странные математические термины. Если вы кладете колесо у внешнего края круга, то узор представляет собой эпитрохоиду. Он выглядит как серия кривых, которая устремляется сначала к краю круга, а потом обратно. С другой стороны, если вы кладете колесо внутрь круга, то узор представляет собой гипотрохоиду, он может напоминать морскую звезду, звезду или пятиугольник с вогнутыми сторонами. Обе кривые являются примером рулетты, кривой, которая образуется, когда фигура перекатывается по неподвижной поверхности и точка на этой фигуре оставляет вихляющую линию. (Фигура не обязательно должна быть кругом.)
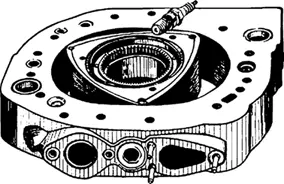
Корпус, в котором находится роторно-поршневой двигатель Ванкеля – движущая сила некоторых автомобилей Mazda, имеет форму эпитрохоиды. Этот двигатель был создан Феликсом Ванкелем, немецким инженером, который получил свой первый патент за устройство в 1929 году. В отличие от поршневых двигателей, двигатель Ванкеля имеет лишь одну движущуюся часть: вращающаяся часть имеет форму треугольника со слегка закругленными краями.
4.14. Поиск внеземного разума берет свое начало в математике
Математическое понятие: теория вероятности
В данный момент огромная группа телескопов к северу от Сан-Франциско находится в поисках признаков внеземных цивилизаций в небе. Названная в честь Пола Аллена, бывшего исполнительного директора Microsoft, который способствовал его изобретению, антенная решетка Аллена содержит 42 радиотелескопа, каждый из которых имеет диаметр 6,1 метра. (Существуют планы собрать 350 таких телескопов.) Телескопы использует SETI, организация в Маунтин-Вью в Калифорнии, которая занимается поиском внеземного разума. Когда все отдельные телескопы будут на месте, они будут покрывать территорию в 1 гектар, или 10 000 квадратных метров.
Читать дальшеИнтервал:
Закладка:










