Иэн Стюарт - Математические головоломки профессора Стюарта

– Отсюда прорехи в вашем пальто и на брюках, а также следы зубов у вас на ноге. Я вижу, что они нанесены ирландским сеттером, ретривером и метисом бульдога с ирландским волкодавом. Хромым на переднюю левую лапу.

– Ах!

– В красном кожаном ошейнике. С колокольчиком. Который заржавел и больше не звонит. Хватило ли у вас наблюдательности, чтобы заметить, сколько времени ушло у собак на бег к точке встречи?

– Я забыл вынуть свои карманные часы, Сомс.

– Да ладно, Ватсап! Вы смотрите, но не видите . Однако в данном случае это время можно вычислить по уже установленным данным.

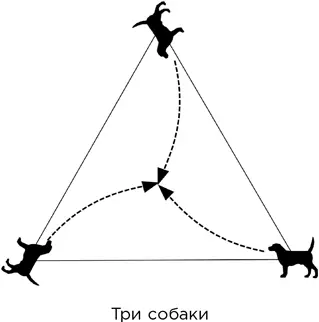
Считайте собак точечными объектами. Ответ см. в главе «Загадки разгаданные».

У лесничих есть один старый прием, позволяющий оценить высоту дерева, не влезая на него и не пользуясь геодезическими инструментами. Этот прием может послужить прекрасным средством взломать лед и оживить атмосферу на пикнике, если где-нибудь поблизости найдется подходящее дерево. Я познакомился с этим трюком в статье Тоби Бакленда [23] Toby Buckland, Digging deeper, Amateur Gardening (20 October 2012), p. 59. . Проделывать этот фокус рекомендуется в брюках.

Встаньте на некотором расстоянии от дерева спиной к нему. Наклонитесь и взгляните на дерево между своими ногами. Если вы не видите его вершины, отойдите подальше и повторяйте процедуру до тех пор, пока не увидите. Если вы легко видите ее, подойдите поближе на такое расстояние, чтобы вершина была едва видима. В этой точке расстояние от вас до основания дерева будет приблизительно равно его высоте.

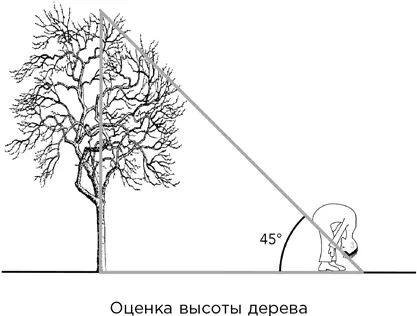
Эта методика, если ее можно так назвать, представляет собой простое приложение евклидовой геометрии. Она основана на том, что большинство людей может посмотреть между ногами назад и вверх под углом примерно 45°. Поэтому линия взгляда на вершину дерева оказывается гипотенузой равнобедренного прямоугольного треугольника, две другие стороны которого равны.

Очевидно, точность этого метода напрямую зависит от гибкости вашего тела, но для многих из нас он дает не слишком большую ошибку. Бакленд замечает: «Попробуйте, это дешевле, чем занятия йогой, и открывает нам взгляд на мир с такого ракурса, с какого большинство из нас не видело его с детства!»

Бог ты мой! Кажется, у всех вокруг больше друзей, чем у меня!

Такое можно встретить и в «Фейсбуке», и в «Твиттере». Такое можно встретить на сайте любой социальной сети, но такое происходит и в реальной жизни. Это случается, если вы вдруг решаете произвести подсчет деловых или сексуальных партнеров. Начиная перебирать своих друзей, чтобы посмотреть, сколько друзей у них , получаешь весьма поучительный опыт. Мало того, что у большинства из них друзей оказывается больше, чем у вас; в среднем у всех без исключения оказывается больше друзей.

Почему же вы так непопулярны в сравнении со всеми остальными? Это внушает серьезную тревогу. Но расстраиваться нет никаких причин. Друзья большинства людей имеют больше друзей, чем сами эти люди.

Вероятно, это звучит по меньшей мере странно. Каждый в данной социальной сети имеет в среднем одно и то же число друзей; говоря конкретно, среднее существует только одно. У кого-то друзей больше, у кого-то меньше, но в среднем их… среднее количество. В этом случае кажется интуитивно правдоподобным, что и друзья этих людей в среднем тоже имеют это же число друзей. Но так ли это?

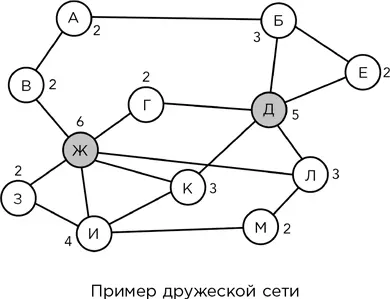
Рассмотрим пример. Он не придуман специально так, чтобы создать нестандартную ситуацию; это первое, что пришло мне в голову. Большинство сетей ведет себя точно так же. В сети (см. выше) представлено 12 человек, линии соединяют друзей. (Считаем, что все дружбы взаимны. В социальных сетях это не всегда так, но эффект, о котором идет речь, все равно возникает.) Представим несколько ключевых показателей в табличной форме.

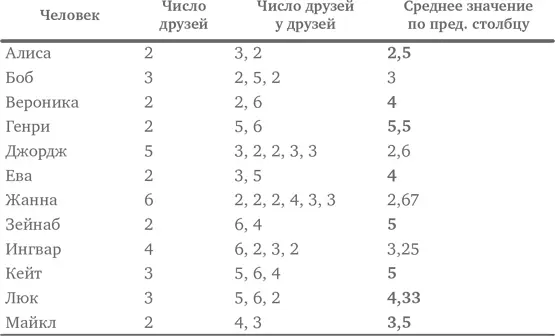
Жирным шрифтом я выделил в последнем столбце числа, которые оказались больше, чем число во втором столбце. Это те случаи, в которых друзья X имеют в среднем больше друзей, чем сам X. Выделены 8 из 12 чисел в этом столбце, и еще в одном случае числа там и там одинаковы.

Если усреднить числа во втором столбце, получится 3. Это означает, что среднее число друзей у человека по всей социальной сети равно 3. Но большинство записей в четвертом столбце больше этого среднего значения. Что в данном случае не так с интуицией?

Ответ дают такие люди, как Джордж и Жанна, у которых особенно (и необычно) много друзей – в данном случае 5 и 6 соответственно. По этой причине при подсчете друзей у друзей их считают намного чаще, чем остальных. И поэтому они вносят больший вклад в сумму в столбце 3 и, следовательно, в среднее значение. С другой стороны, люди с небольшим числом друзей фигурируют в подсчете гораздо реже и вносят значительно меньший вклад.

Ваши друзья – не типичный пример. Среди них гораздо лучше представлены люди с большим числом друзей, поскольку шанс на то, что вы входите в число их друзей, намного выше. А люди с небольшим числом друзей представлены куда хуже. Именно этот эффект сдвигает среднее число друзей у друзей в сторону увеличения.

В третьем столбце таблицы можно увидеть, как это происходит. Число 5 фигурирует в столбце 3 пять раз – по одному у каждого из друзей Джорджа; точно так же 6 в столбце 3 встречается шесть раз, по одному у каждого из друзей Жанны. С другой стороны, вклад Алисы в столбец 3 (не в ее собственной строке, а в тех случаях, когда она сама фигурирует в других строках как друг) составляет всего лишь две двойки: одна от Боба и одна от Вероники. Таким образом, вклад Джорджа составляет 25, а вклад Жанны – даже 36, тогда как бедняжка Алиса вносит всего лишь 4.

Кому дано, приумножится.

Во втором столбце ничего подобного не происходит: каждый вносит в среднее значение, равное 3, свою справедливую долю.

На самом деле среднее значение всех чисел в столбце 4 равно 3,78, заметно больше трех. Вероятно, мне следовало бы использовать взвешенное среднее значение: сложить все числа в столбце 3 и разделить на их количество. Тогда получится 3,55, все равно больше трех.

Надеюсь, после моего объяснения вы почувствовали себя лучше.