Иэн Стюарт - Математические головоломки профессора Стюарта

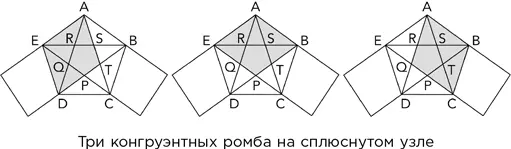
– Потому что CD и BE не совпадают с краями бумажной полоски, так что мы не можем пока сказать то же о ромбах CDRB или DESC. Вот почему я не провел линии CD.

Я, надо признаться, этого не заметил.

– В таком случае это невероятно тонкий момент, Сомс. Мало того, наше утверждение может оказаться попросту неверным!

Он почему-то вздохнул.

– Теперь мы переходим к центральному пункту моих рассуждений. Диагонали ромба рассекают его углы пополам, а противоположные углы равны, – Сомс отметил четыре угла греческой буквой θ (тета), см. рисунок слева.

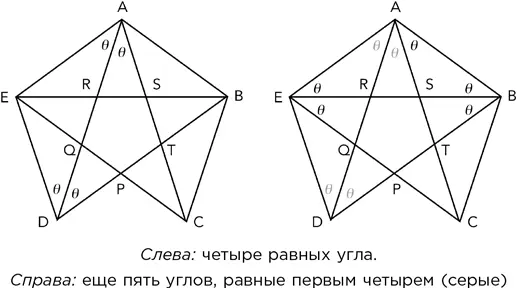
По сходным причинам угол CAB также равен θ. Поскольку ромбы DEAT и PEAB конгруэнтны, я могу отметить буквой θ еще четыре угла. Получается рисунок справа.

– А теперь, Ватсап, скажите: что при взгляде на этот рисунок сразу же приходит в голову?

– На нем чертовски много букв θ, – без промедления отозвался я.

Он недовольно поморщился, и я услышал, как в горле у него что-то негромко зарокотало, не знаю уж почему.

– Это же очевидно, как шея высоченного жирафа, Ватсап! Посмотрите на треугольник EAB.

Я нашел треугольник и внимательно рассмотрел его, поначалу ничего не понимая. Ну… В этом треугольнике тоже много отметок θ. Так, так… все его углы составлены из θ! Теперь я понял.

– Сумма углов треугольника равна 180°, Сомс. В этом треугольнике углы равны θ, θ и 3θ. Их сумма 5θ равна 180°, а значит, θ = 36°.

– Когда-нибудь из вас еще получится геометр, – сказал Сомс. – Остальное доказывается легко. Отрезки DE, EA, AB и BC равны по длине, поскольку являются сторонами конгруэнтных ромбов. Углы ÐDEA, ÐEAB и ÐABC равны между собой, поскольку располагаются в конгруэнтных ромбах, и один из них, ÐEAB, равен 3 × θ, то есть 108°. Так что все три угла равны 108°. Но этому же равен внутренний угол правильного пятиугольника.

– Так что точки D, E, A, B, C являются углами правильного пятиугольника, и я могу завершить рисунок, проведя отрезок CD! – воскликнул я. – Как неле… – я поймал краем глаза его взгляд. – Э-э, как элегантно, Сомс!

Он пожал плечами.

– Пустяк, Ватсап. Этого достаточно, чтобы покончить с Матемагической ассоциацией Нумерики и причинить Могиарти некоторые неудобства. Сам же он… Боюсь, он окажется куда более крепким орешком.

E. S. Benilov, C. P. Cummins, and W. T. Lee. Why do bubbles in Guinness sink? arXiv: 1205.5233 [physics. flu-dyn].

– Собаки столкнулись через 10 секунд, – объявил Сомс.

– Поверю вам на слово, – сказал я. – Но удовлетворите мое любопытство: как вы получили эту цифру?

– Задача симметрична, Ватсап, а симметрия зачастую упрощает рассуждения. В описанных вами условиях три собаки всегда находятся в вершинах равностороннего треугольника. Он вращается и одновременно сжимается, но сохраняет форму. Таким образом, с точки зрения одной из собак – скажем, A, – она все время бежит по прямой к соседней собаке B.

– Но разве треугольник не вращается , Сомс?

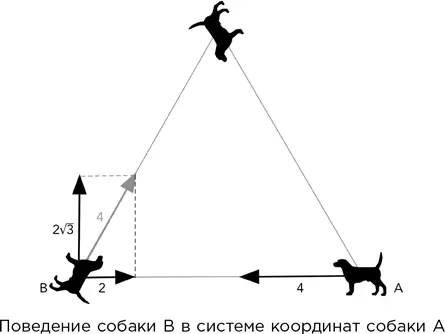
– Вращается, но это несущественно, поскольку мы можем проводить вычисления во вращающейся системе координат. Важно, насколько быстро треугольник сжимается . Собака B всегда бежит под углом 60° к прямой AB, поскольку собаки всегда образуют равносторонний треугольник. Так что компонента ее скорости в направлении собаки A равна 1/2 × 4 = 2 ярда в секунду. Следовательно, A и B приближаются друг к другу с суммарной скоростью 4 + 2 = 6 ярдов в секунду и покрывают разделявшее их в начальный момент расстояние в 60 ярдов за 60/6 = 10 секунд.

Предположим, в социальной сети n человек, причем человек i имеет x i друзей. Тогда среднее число друзей по все членам сети составляет

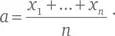
При рассмотрении столбца 3 в таблице – взвешенного среднего от числа друзей у каждого из друзей j человека i – мы используем стандартный математический прием и работаем вместо этого с человеком j . Этот человек фигурирует как друг у x j человек – а именно у собственных друзей – и вносит x j в подсчет полного количества у каждого из этих друзей. Так что случаи, когда человек j выступает в качестве друга, вносят вклад x j² в общую сумму. Число элементов в столбце 3 составляет x 1+ … + x n . Так что взвешенное среднее числа друзей у каждого из друзей равно

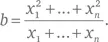
Я утверждаю, что для любых x j мы всегда имеем b>a , если только все x j не равны, в каковом случае b = a . Это следует из стандартного неравенства, связывающего среднее с тем, что инженеры называют «среднеквадратичным значением» (это корень квадратный из среднего значения квадратов):

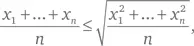
причем равенство достигается только при равенстве всех x j . Возведя в квадрат и сгруппировав, получим a за исключением случая равенства всех x j , что и требовалось. Дополнительную информацию можно найти на сайте

http://www.artofproblemsolving.com/wiki/index.php?title=Root-Mean_Square-Arithmetic_Mean-Geometric_Mean-Harmonic_mean_Inequality

Замечание Сомса – пример применения теории Рамсея – области комбинаторики, названной в честь Фрэнка Рамсея, доказавшего аналогичную, но более общую теорему в 1930 г. Его брат Майкл стал архиепископом Кентерберийским. Подойдем к нашему вопросу с осторожностью. Предположим, что некоторое число людей сидит за столом, причем каждый человек связан с другими либо ножом, либо вилкой. Выберем два произвольных числа f и k . Тогда существует некоторое число R , зависящее от f и k , такое, что если за столом присутствует по крайней мере R человек, то либо f из них соединены вилками, либо k – ножами.

Наименьшее такое R обозначается как R ( f, k ) и называется числом Рамсея. Из доказательства Сомса видно, что R (3,3) = 6. Числа Рамсея вычисляются с необычайным трудом, за исключением нескольких простых случаев. Известно, к примеру, что R (5,5) лежит в промежутке от 43 до 49, но его точное значение остается загадкой.