Саймон Сингх - Симпсоны и их математические секреты

В школьной столовой Мартин проявляет интерес к обеду Лизы, который представляет собой не обычную еду из столовой, а обед в вакуумной упаковке с рисунками на космическую тематику. Когда Лиза поднимает пакет и объясняет, что «такую пищу ест Джон Гленн, если он не в космосе», Мартин замечает на тыльной стороне пакета головоломку. Задача состоит в том, чтобы найти следующий символ в такой последовательности:

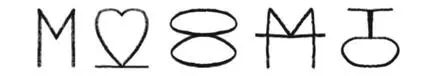
Мартин мгновенно решает головоломку, но Лиза оказывается в тупике. Она все больше и больше расстраивается по мере того, как сидящие вокруг нее ученики, в том числе Барт, заявляют, что готовы назвать следующий символ в последовательности. Создается впечатление, что все могут решить головоломку… кроме Лизы. В итоге девочка всю оставшуюся часть эпизода ставит под сомнение свои умственные способности и научную судьбу. К счастью, вам не придется испытывать таких эмоциональных потрясений. Я предлагаю вам минутку поразмышлять над головоломкой, а затем взглянуть на ответ, представленный ниже.

Головоломка на пакете Лизы заслуживает особого внимания, потому что она помогла укрепить математическую основу мультсериала и сыграла важную роль в привлечении нового математика в команду его авторов. Джей Стюарт Бернс изучал математику в Гарварде, после чего поступил в Калифорнийский университет в Беркли, чтобы получить степень доктора наук. Темой докторской диссертации Бернса должна была стать алгебраическая теория чисел или топология, но он отказался от этой идеи и получил степень магистра вместо степени доктора наук. Причиной преждевременного ухода Бернса из Беркли стало предложение о работе от продюсеров комедийного телесериала Unhappily Ever After («Несчастливы вместе»). Бернс всегда втайне мечтал о карьере сценариста телевизионных комедий, и это был его звездный час. Вскоре Бернс подружился с Дэвидом Коэном, и тот пригласил его в офис «Симпсонов» на вычитку сценария одного из эпизодов, которым как раз и оказался эпизод «Лиза Симпсон». По мере раскрытия сюжета, в том числе сцены с головоломкой, у Бернса формировалось ощущение, что именно здесь его место – рядом с Коэном и другими авторами «Симпсонов» из числа математиков. Когда Бернс работал в сериале «Несчастливы вместе», его считали гиком с дипломом магистра. Напротив, когда он присоединился к команде «Симпсонов», его магистерская степень перестала быть исключением. И навешенный на него ярлык ботаника сменила слава специалиста по тонкому юмору.

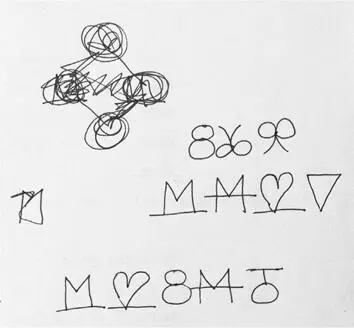
Хотя Дэвид Коэн не может вспомнить, кто именно предложил головоломку из эпизода «Лиза Симпсон», но первые наброски сделал он. Эта головоломка почти в таком же виде, как в эпизоде, отображена в нижней строке страницы с рисунками. Для того чтобы решить задачу, необходимо обратить внимание на то, что правая и левая половины каждого символа представляют собой зеркальное отображение друг друга. Правая часть первого символа – это цифра 1, а левая – ее зеркальное отображение. Правая часть второго символа – цифра 2, а левая – ее отображение. То же самое касается третьего, четвертого и пятого символов, а значит, шестым символом должна быть цифра 6 вместе со своим зеркальным отображением.

Верхняя строка говорит о том, что Коэн планировал использовать последовательность цифр 3, 6 и 9, но отбросил эту идею, вероятно, потому, что четвертый элемент последовательности (12) состоял бы из двух цифр. Средняя строка, в которой показана последовательность цифр 1, 4, 2 и 7, тоже не нашла поддержки, так как не совсем понятно, каким был бы ее пятый элемент, а сам Коэн уже не помнит, что он имел в виду.

Фотографию предоставил Дэвид Коэн

Рассказав мне историю о том, как его взяли в команду «Симпсонов», Бернс провел параллели между головоломками и шутками, заявив, что у них много общего. И головоломка, и шутка представляют собой тщательно продуманную схему; в обоих случаях происходит неожиданный поворот и есть кульминация. В действительности и головоломки, и шутки заставляют вас размышлять и улыбаться в тот момент, когда вы понимаете, в чем дело. Возможно, именно этим отчасти объясняется тот факт, что математики оказались столь ценными членами команды сценаристов мультсериала «Симпсоны» и привнесли в его создание не только любовь к математике, но и новый подход к работе. Бернс и раньше замечал, что его коллеги-нематематики, как правило, предлагают полностью сформированные остроты, созданные в момент вдохновения, тогда как математики из команды «Симпсонов» склонны предлагать спонтанные идеи для шуток, а затем обсуждать их до тех пор, пока не будет найден требуемый вариант.

На такой групповой подход математики полагаются и при создании сюжетных линий. По словам Джеффа Уэстбрука, коллеги Бернса по «Симпсонам» и еще одного экс-математика, подобное стремление к сотрудничеству берет начало в их предыдущей карьере: «Я был теоретиком в области компьютерных наук, а это означало, что мы с коллегами вместе доказывали множество математических теорем. Когда я пришел сюда, то с удивлением обнаружил, что примерно то же самое происходит и в комнате сценаристов, поскольку мы так же сидим и выдвигаем свои идеи. Во всем этом присутствует некая общая творческая нить, помогающая решить задачу. В одном случае это математическая теорема, в другом – поворот сюжета. Нам необходимо разбить сюжет на составляющие и проанализировать его развитие. О чем вообще идет речь в этой истории?»

Взяв себе на заметку сказанное Уэстбруком, я начал спрашивать других авторов «Симпсонов», почему, по их мнению, многие сценаристы с математическими наклонностями нашли в сериале свой дом. Как объяснил Дэвид Коэн, потому что они более уверенно и комфортно себя чувствуют в ходе исследования чего-то неизведанного, вооружившись только интуицией: «Процесс доказательства чего-то сродни процессу написания сценария для комедии, поскольку в обоих случаях вы не можете быть уверены, что достигнете конечной цели. Когда вы пытаетесь придумать шутку из ничего (при этом она должна отражать определенную тему или рассказывать определенную историю), нет никаких гарантий, что таковая вообще существует, к тому же будет смешной и поможет вам реализовать задуманное. Точно так же, когда вы пытаетесь доказать что-то в математике, велика вероятность, что это просто недоказуемо. Безусловно, достаточно велика вероятность и того, что нет доказательства, доступного человеческому пониманию. В обоих случаях (поиска шутки и доказательства теоремы) интуиция подсказывает вам, стоят ли ваши усилия потраченного времени».