Яков Перельман - Живая математика. Математические рассказы и головоломки

Каждый из 9 вновь узнавших поделился в ближайшие четверть часа с 3 другими гражданами, так что в 8 3/ 4утра новость стала известна

13 + (3 х 9) = 40 гражданам.

Если слух распространяется по городу и далее таким же способом, т. е. каждый, узнавший новость, успевает в ближайшие четверть часа сообщить ее 3 согражданам, то осведомление города будет происходить по следующему расписанию:

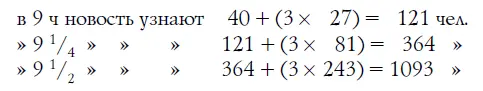
Спустя полтора часа после первого появления в городе новости ее будут знать, как видим, всего около 1100 человек. Это, казалось бы, немного для населения в 50 000. Можно подумать, что новость не скоро еще станет известна всем жителям. Проследим, однако, далее за распространением слуха:

Рис. 61. В половине одиннадцатого все жители города осведомлены о новости, которая в 8 ч утра того же дня была известна лишь одному человеку

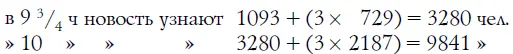
Еще спустя четверть часа будет осведомлено уже больше половины города:

9841 + (3 х 6561) = 29 524.

И, значит, к половине одиннадцатого того же дня поголовно все жители большого города будут осведомлены о новости, которая в 8 ч утра известна была только одному человеку.

Проследим теперь, как выполнен был предыдущий подсчет. Он сводился, в сущности, к тому, что мы сложили такой ряд чисел:

1 + 3 + (3 х 3) + (3 х 3 х 3) + (3 х 3 х 3 х 3) и т. д.

Нельзя ли узнать эту сумму как-нибудь короче, наподобие того, как определяли мы раньше сумму чисел ряда 1+2 + 4 + 8 и т. д.?

Это возможно, если принять в соображение следующую особенность складываемых здесь чисел:

1 = 1

3 = 1 х 2 + 1

9 = (1 + 3) х 2 + 1

27 = (1 + 3 + 9) х 2 + 1

81 = (1 + 3 + 9 + 27) х 2 + 1

и т. д.

Иначе говоря, каждое число этого ряда равно удвоенной сумме всех предыдущих чисел плюс единица.

Отсюда следует, что если нужно найти сумму всех чисел нашего ряда от 1 до какого-либо числа, то достаточно лишь прибавить к этому последнему числу его половину (предварительно откинув в последнем числе единицу).

Например, сумма чисел

1 + 3 + 9 + 27 + 81 +243 + 729

равна 729 + половина от 728, т. е. 729 + 364 = 1093.

В нашем случае каждый житель, узнавший новость, передавал ее только трем гражданам. Но если бы жители города были еще разговорчивее и сообщали услышанную новость не 3, а, например, 5 или даже 10 другим, слух распространялся бы, конечно, гораздо быстрее. При передаче, например, пятерым картина осведомления города была бы такая:

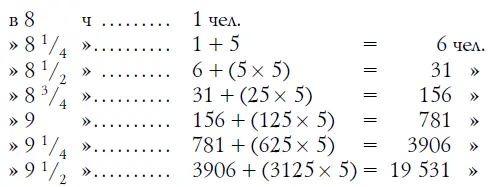
Ранее чем в 9 3/ 4ч утра новость будет уже известна всему 50-тысячному населению города.

Еще быстрее распространится слух, если каждый, услышавший новость, передаст о ней 10 другим. Тогда получим такой любопытный, быстро возрастающий, ряд чисел:

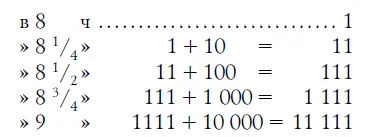
Следующее число этого ряда, очевидно, есть 111 111. Это показывает, что весь город узнает про новость уже в самом начале 10-го часа утра. Слух разнесется почти в один час!

В дореволюционные годы были у нас - а за рубежом, вероятно, и теперь еще находятся - предприниматели, которые прибегают к довольно оригинальному способу сбывать свой товар, обычно посредственного качества. Начинали с того, что в распространенных газетах и журналах печатали рекламу такого содержания:

Немало людей, конечно, соблазнялись заманчивым объявлением и просили прислать условия необычной покупки. В ответ на запрос они получали подробный проспект, из которого узнавали следующее.

За 10 руб. высылался пока не сам велосипед, а только 4 билета, которые надо было сбыть по 10 руб. своим четверым знакомым. Собранные таким образом 40 руб. следовало отправить фирме, и тогда лишь прибывал велосипед; значит, он обходился покупателю действительно всего в 10 руб., остальные 40 руб. уплачивались ведь не из его кармана. Правда, кроме уплаты 10 руб. наличными деньгами, приобретатель велосипеда имел некоторые хлопоты по продаже билетов среди знакомых, но этот маленький труд в счет не шел.

Что же это были за билеты? Какие блага приобретал за 10 руб. их покупатель? Он получал право обменять их у фирмы на 5 таких же билетов; другими словами, он приобретал возможность собрать 50 руб. для покупки велосипеда, который ему обходился, следовательно, только в 10 руб., т. е. в стоимость билета. Новые обладатели билетов, в свою очередь, получали от фирмы по 5 билетов для дальнейшего распространения и т. д.

На первый взгляд во всем этом не было обмана. Обещание рекламного объявления исполнялось; велосипед в самом деле обходился покупателям всего лишь в 10 руб. Да и фирма не оказывалась в убытке - она получала за свой товар полную его стоимость.

А между тем вся затея - несомненное мошенничество. «Лавина», как называли эту аферу у нас, или «снежный ком», как величали ее французы, вовлекала в убыток тех многочисленных ее участников, которым не удавалось дальше сбыть купленные ими билеты. Они-то и уплачивали фирме разницу между 50-рублевой стоимостью велосипедов и 10-рублевой платой за них. Рано ли, поздно ли, но неизбежно наступал момент, когда держатели билетов не могли найти охотников их приобрести. Что так должно непременно случиться, вы поймете, дав себе труд с карандашом в руке проследить за тем, как стремительно возрастает число людей, вовлекаемых в лавину.

Первая группа покупателей, получившая свои билеты прямо от фирмы, находит покупателей обычно без особого труда: каждый член этой группы снабжает билетами четверых новых участников.

Эти четверо должны сбыть свои билеты 4 х 5, т. е. 20 другим, убедив их в выгодности такой покупки. Допустим, что это удалось и 20 покупателей завербовано. Лавина движется дальше, 20 новых обладателей билетов должны наделить ими 20 х 5 = 100 других.

До сих пор каждый из «родоначальников» лавины втянул в нее

1 + 4 + 20 + 100 = 125 человек,

из которых 25 имеют по велосипеду, а 100 - только надежду его получить, уплатив за эту надежду по 10 руб. Теперь лавина выходит уже из тесного круга знакомых между собою людей и начинает растекаться по городу, где ей становится, однако, все труднее и труднее отыскивать свежий материал. Сотня последних обладателей билетов должна снабдить такими же билетами 500 граждан, которым, в свою очередь, придется завербовать 2500 новых жертв. Город быстро наводняется билетами, и отыскивать охотников приобрести их становится весьма нелегким делом.