Жюль Пуанкаре - Теорема века. Мир с точки зрения математики

Итак, прежде всего надо определить равенство двух сил. Когда говорят, что две силы равны? Тогда, отвечают нам, когда, будучи приложены к одной и той же массе, они сообщают ей одно и то же ускорение или когда, будучи прямо противоположно направлены, они взаимно уравновешиваются. Но это определение совершенно призрачно. Силу, приложенную к данному телу, нельзя отцепить от него и прицепить затем к другому телу вроде того, как отцепляют локомотив, чтобы сцепить его с другим поездом. Поэтому и нельзя знать, какое ускорение данная сила, приложенная к данному телу, сообщила бы другому телу, если бы была к нему приложена. Нельзя также знать, каково было бы действие двух сил, не прямо противоположных, в том случае, если бы они были прямо противоположны.

Это именно определение и стараются, так сказать, материализовать, когда измеряют силу динамометром или уравновешивают ее грузом. Две силы F и F’ , которые я для простоты предположу вертикальными и направленными снизу вверх, приложены соответственно к двум телам С и С’ ; я подвешиваю одно и то же тело веса Р сначала к телу С , потом к С’ ; если в обоих случаях имеет место равновесие, то я заключу, что две силы F и F’ , будучи обе равны весу Р , равны между собою.

Но уверен ли я, что тело Р сохранило тот же вес, когда я перенес его от первого тела ко второму? Вовсе нет, я уверен как раз в противном; я знаю, что напряжение силы тяжести меняется при переходе от одной точки к другой и что оно, например, больше на полюсе, чем на экваторе. Бесспорно, эта разница ничтожна, и на практике я не стал бы принимать ее в расчет; но правильное определение должно обладать математической точностью, а этой точности здесь нет. Сказанное относительно тяжести, очевидно, применимо и к упругой силе динамометра, которая может меняться в зависимости от температуры и от многих других обстоятельств.

Это не все: нельзя сказать, что вес тела Р приложен к телу С и прямо уравновешивает силу F . То, что приложено к телу С , есть действие А тела Р на тело С ; тело Р в свою очередь находится под действием, с одной стороны, своего собственного веса, с другой – противодействия R тела С на тело Р . В результате сила F равна силе A , потому что уравновешивает ее; сила А равна R в силу принципа равенства действия противодействию; наконец, сила R равна весу Р , потому что его уравновешивает. Уже как следствие этих трех равенств мы выводим равенство F и веса Р .

Таким образом, при определении равенства двух сил нам приходится опираться на принцип равенства действия и противодействия; значит, этот последний принцип мы должны считать уже не как экспериментальный закон, а как определение.

Итак, устанавливая равенство двух сил, мы пользуемся двумя правилами: равенством двух взаимно уравновешивающихся сил и равенством действия противодействию. Но выше мы видели, что этих двух правил недостаточно; мы вынуждены прибегнуть к третьему правилу и допустить, что некоторые силы, как, например, вес тела, постоянны по величине и направлению. Но это третье правило, как я сказал, представляет собой экспериментальный закон и оно верно лишь приближенно; опирающееся на него определение – плохое определение.

Итак, нам приходится вернуться к определению Кирхгофа: сила равна массе, умноженной на ускорение. Теперь этот «закон Ньютона» выступает уже не как экспериментальный закон, а только как определение. Но это определение еще недостаточно, так как мы не знаем, что такое масса. Правда, он позволяет нам вычислить отношение двух сил, приложенных к одному и тому же телу в разные моменты, но он ничего не сообщает нам об отношении двух сил, приложенных к двум различным телам.

Для дополнения его придется снова прибегнуть к третьему закону Ньютона (равенство действия и противодействия), рассматривая последний опять-таки не как экспериментальный закон, а как определение. Два тела А и В действуют друг на друга; ускорение А , умноженное на массу А , равно действию В на А , таким же образом, произведение ускорения В на его массу равно противодействию А на В . И так как по определению действие равно противодействию, то массы А и В будут обратно пропорциональны ускорениям двух этих тел. Этим отношение наших двух масс определено, и дело опыта – проверить, что это отношение постоянно.

Все было бы хорошо, если бы два тела А и В были единственными, с которыми приходится считаться, и были изолированы от действия остального мира. Но этого нет; ускорение тела A зависит не только от действия тела В , но и от действия множества других тел: С, D и т. д. Поэтому, чтобы применить предыдущее правило, нужно было бы разложить ускорение тела A на несколько составляющих и выделить из них ту, которая обусловлена действием тела В .

Это разложение было бы еще возможно, если бы мы допустили , что действие С на А просто прикладывается к действию В на А , так что присутствие тела С не изменяет действия В на А и присутствие В не изменяет действия С на А ; следовательно, если бы мы допустили, что любые два тела притягиваются, что их взаимное действие направлено по соединяющей их прямой и зависит только от их расстояния, словом – если бы мы допустили гипотезу центральных сил.

Известно, что для определения масс небесных тел пользуются совершенно иным принципом. Закон тяготения учит нас, что притяжение двух тел пропорционально их массам; если r есть расстояние между ними, m и m’ – их массы, K – некоторая постоянная, то притяжение их будет равно

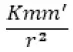
То, что измеряют в этом случае, не есть масса как отношение силы к ускорению – это есть масса притягивающая; это – не инерция тела, а его притягательная способность.

Применение такого косвенного приема не является теоретически необходимым. Легко могло бы случиться, что притяжение было бы обратно пропорционально квадрату расстояния, не будучи пропорционально произведению масс; оно равнялось бы

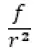
Но равенство:

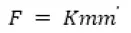
не имело бы смысла. При таких условиях все-таки было бы возможно на основании наблюдений над относительными движениями небесных тел измерять их массы.

Но имеем ли мы право допускать гипотезу центральных сил? Верна ли она в точности? Можно ли быть уверенным, что она никогда не окажется в противоречии с опытом? Кто взял бы на себя смелость утверждать это? А ведь если нам придется оставить эту гипотезу, то рушится и все здание, воздвигнутое с таким трудом. И тогда мы уже не имеем более права говорить о составляющей ускорения А , зависящей от действия В . Мы не имеем никакого средства отличить ее от той, которая обусловлена действием С или другого тела. Правило для измерения масс становится неприложимым.