Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]

Вездесущность уравнений в частных производных

Применение анализа в современной науке – это в значительной степени упражнение по формулировке, решению и интерпретации уравнений в частных производных. Уравнения Максвелла для электромагнитных волн – это уравнения в частных производных. Таковы же законы упругости, акустики, теплопередачи, текучести и газовой динамики. Список можно продолжать: модель Блэка – Шоулза для определения теоретической цены опционов [288]или модель Ходжкина – Хаксли [289], описывающая распространение электрических импульсов по нервным волокнам, – все это тоже уравнения в частных производных.

Даже на переднем крае современной физики математическую инфраструктуру по-прежнему обеспечивают дифференциальные уравнения в частных производных. Обратимся к общей теории относительности Эйнштейна [290]. Она переосмысливает гравитацию как проявление кривизны четырехмерной ткани пространства-времени. Стандартная метафора предлагает нам представить пространство-время как эластичную деформируемую ткань наподобие поверхности батута. В обычном состоянии она туго натянута, но если положить на нее нечто тяжелое, скажем, шар для боулинга, то она может изгибаться. Точно так же массивное небесное тело, например Солнце, может изгибать вокруг себя ткань пространства-времени. Теперь вообразите нечто гораздо меньшее, допустим, маленький шарик (изображающий планету), который катится по искривленной поверхности батута. Поскольку она прогибается под весом шара для боулинга, она искривляет траекторию шарика. Вместо того чтобы двигаться по прямой линии, он следует контурам искривленной поверхности и вращается вокруг шара для боулинга. Вот почему, по словам Эйнштейна, планеты двигаются вокруг Солнца. Они не ощущают никакой силы, а просто следуют по пути наименьшего сопротивления в искривленной ткани пространства-времени.

Какой бы непостижимой ни была эта теория, в ее математической основе лежат уравнения в частных производных. То же самое верно для квантовой механики, теории микромира. Ее основное уравнение – уравнение Шрёдингера [291] – тоже использует частные производные. В следующей главе мы подробнее рассмотрим такие уравнения, чтобы вы имели представление о том, что это такое, откуда они берутся и почему так важны для повседневной жизни. Как мы увидим, уравнения в частных производных не только описывают остывающую на столе тарелку супа, но и объясняют, как он нагревается в микроволновой печи.

До начала 1800-х понятие тепла оставалось загадкой. Что это такое? Может, жидкость, похожая на воду? Казалось, это действительно текучая субстанция, но вы не могли ни подержать ее в руках, ни увидеть. Вы могли измерить тепло косвенно, отслеживая температуру горячего предмета по мере его остывания, но никто не знал, что происходит внутри остывающего предмета.

Секреты тепла раскрыл человек, который часто ощущал холод. Осиротев в девятилетнем возрасте, Жан-Батист Фурье [292], будучи подростком, страдал астматическим расстройством. Повзрослев, он пришел к выводу, что тепло важно для здоровья. Он поддерживал высокую температуру в своей комнате и даже летом кутался в теплую одежду. Фурье был одержим теплом во всех аспектах своей научной деятельности. Он создал концепцию глобального потепления и первым объяснил, как парниковый эффект регулирует среднюю температуру Земли.

В 1807 году Фурье использовал анализ для решения задачи теплопроводности [293]. Он вывел уравнение в частных производных, которое позволяло ему предсказывать изменение температуры остывающего предмета, скажем предварительно раскаленного железного стержня. Он обнаружил, что может решить такую задачу, как бы неравномерно ни распределялась температура по длине стержня на момент начала охлаждения. Стержень мог иметь горячие и холодные места, но аналитический метод Фурье без проблем справлялся с задачей.

Представьте себе длинный тонкий цилиндрический железный стержень, неравномерно нагретый в кузнечном горне, так что по всей его длине одни его участки горячие, а другие – холодные. Для простоты предположим, что вокруг стержня есть идеально изолирующая муфта, не позволяющая теплу уходить, поэтому единственный путь его передачи – распространение вдоль по стержню от горячих участков к холодным. Фурье постулировал (и эксперименты подтвердили это), что скорость передачи тепла в данной точке стержня пропорциональна разности температуры в этой точке и средней температуры соседних точек. Когда я говорю о соседних точках , я действительно говорю о соседях – вообразите две точки по сторонам от нашей, где каждая к ней бесконечно близка.

В этих идеализированных условиях физика теплопередачи проста. Если точка холоднее соседей, она нагревается. Если горячее – остывает. Чем сильнее перепад температур, тем быстрее температура выравнивается. Если температура в точке равна средней температуре соседей, все уравновешивается и теплопередача не происходит, температура точки в следующий момент останется той же.

Этот процесс сравнения мгновенной температуры точки с мгновенной температурой ее соседей привел Фурье к уравнению в частных производных, которое сегодня известно как уравнение теплопроводности. Оно включает производные по двум независимым переменным: время ( t ) и положение на стержне ( x ).

Самая сложная часть задачи, которую поставил перед собой Фурье, состояла в беспорядочном исходном распределении горячих и холодных точек на стержне. Чтобы решить ее, Фурье предложил схему, которая казалась безумно оптимистичной, но почти безрассудной. Он утверждал, что любое исходное распределение температуры можно заменить эквивалентной суммой простых синусоид.

Синусоиды стали его строительными блоками. Он выбрал их, потому что они упрощали задачу. Он знал, что если исходная температура подчинялась синусоидальной закономерности, то и по мере остывания это свойство будет сохраняться.

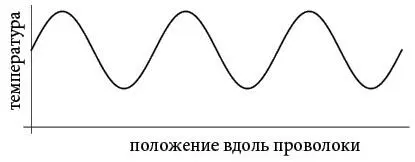
В этом был ключ: синусоиды не двигаются. Они просто остаются на месте. Правда, они затухали по мере того, как их горячие точки остывали, а холодные нагревались, но с этим легко было справиться: это просто означало, что колебания температуры со временем уменьшаются. Как показано на следующем рисунке, распределение температуры, первоначально представленное пунктирной синусоидой, постепенно уменьшает размах и превращается в сплошную синусоиду.

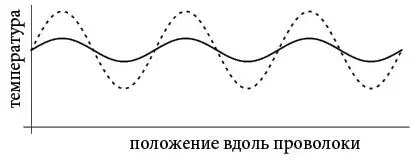
Важно было то, что во время такого сглаживания синусоидальные волны оставались неподвижны. Они были стоячими волнами .