М. Л. Фартушняк - Репетитор по математике. Арифметика

Для удобства чтения и запоминания больших чисел их разбивают на классы. Справа отделяют три цифры (первый класс), потом ещё три цифры (второй класс) и т. д. Между собой классы отделяются небольшим пробелом. Первый класс даёт число единиц, второй – число тысяч, третий – миллионов. Каждая из цифр класса наз. его разрядом, счёт разрядов также идёт справа. Числа в первом классе справа налево: единицы, десятки, сотни, во втором классе соответственно: тысячи, десятки тысяч, сотни тысяч. В третьем классе: миллионы, десятки миллионов, сотни миллионов. Единица четвёртого класса называется миллиардом, пятого триллионом. Существует единица и для 6, 7, 8 и т. д. классов, но мы их рассматривать не будем. А теперь поупражняемся.

Таблица 1

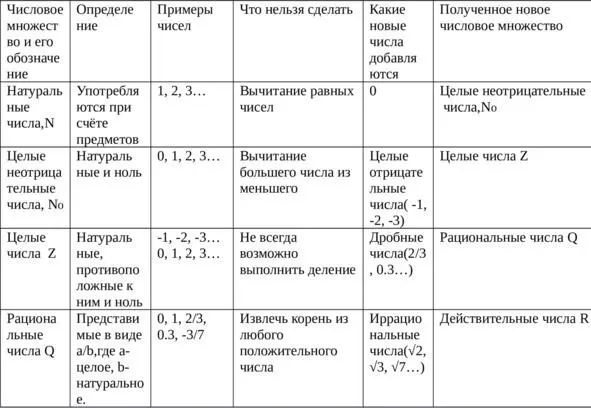
35 461 298 читается так: 35 миллионов 461 тысяча 298.

Не следует бояться больших чисел, число 12 021 306 200 025 имеет 5 классов, поэтому читается таким образом: 12 триллионов 21 миллиард 306 миллионов 200 тысяч 25.

Теперь перейдём непосредственно к арифметическим действиям. Мы не будем давать здесь определений арифметических действий, они известны всем. Итак, арифметические действия – это сложение, вычитание, умножение и деление, а также возведение в степень и извлечение корня. Степени и корни изучаются в курсе алгебры и мы их рассматривать не будем. Здесь приведём примеры основных арифметических действий:

Сложение.

8 +5 = 13. Здесь 8 и 5 – слагаемые, 13 – сумма.

Вычитание.

15 – 8 = 7. Здесь 15 – уменьшаемое, 8 – вычитаемое, 7 – разность.

Умножение.

6 × 5 = 30. Здесь 6 – множимое, 5 – множитель, 30 – произведение.

Деление.

30 ÷ 6 = 5. Здесь 30 – делимое, 6 – делитель, 5 – частное.

Эти термины нам понадобятся в дальнейшем.

Важнейшим понятием арифметики есть порядок действий. При вычислениях им нельзя игнорировать. Поэтому 4—2+1 будет равно трём если проводить действия в порядке их записи. Если же сначала сложить 2+1 и вычесть полученную сумму из 4, то получим совсем другой ответ, которой равен единице. Чтобы указать в каком порядке нужно выполнять действия пользуются скобками. Действие, заключённое в скобки, выполняется раньше других. Таким образом, порядок действий при вычислениях:

1. Сначала выполняются действия, заключённые в скобки. Умножение и деление делается в порядке их следования, но раньше, чем сложение и вычитание.

2. Затем выполняются оставшиеся действия, причём опять умножение и деление делается в порядке их следования, но раньше сложения и вычитания.

Рассмотрим пару примеров: (2+4) ×5.

Сначала вычисляем действие в скобках 2+4 = 6, далее следует умножение на 5:

6×5 = 30.

Это простой пример. Рассмотрим более сложный:

9+16:4—2 × (16—2×7+4) +6 × (2+5)

Сначала выполняем действия в скобках, не забывая о том, что умножение и деление идёт впереди сложения и вычитания.

Первая скобка: 2 × 7 = 14, 16 – 14 = 2, 2 +4 = 6.

Вторая скобка: 2 +5 = 7.

Наш пример примет вид: 9 +16: 4 – 2 × 6 +6 × 7. Теперь выполняем операции умножения и деления в порядке их следования:

16: 4 = 4, 2 × 6 = 12, 6 × 7 = 42.

И окончательно, выполняем операции сложения и вычитания в порядке их следования. Имеем 9 +4 – 12 +42 = 43.

Иногда приходится заключать скобки в скобки, поэтому пользуются ещё и квадратными скобками.

Порядок действий: сначала выполняются в круглых скобках, потом в квадратных, а потом все остальные действия. Например,

5+2× [14—3× (8—6)] +32: (10—2×3)

Выполняем действия в круглых скобках, имеем:

8 – 6 = 2, 10 – 2 × 3 = 10 – 6 = 4

Действия в квадратных скобках дают: 14 – 3 × 2 = 8

Выполняя оставшиеся действия, имеем:

5 +2 × 8 +32: 4 = 5 +16 +8 = 29.

А теперь немного отвлечёмся. Сейчас в соц. сетях некоторые пользователи придумывает такое развлечение, они выкладывают простой арифметический пример и просят других пользователей дать правильный ответ. Вот, например,

10:2 (4—2).

Наиболее часто встречающиеся ответы 10 и 2.5. Вы уже немного продвинулись в арифметике и поэтому для вас не составит труда дать правильный ответ. Это число 10. 70％ пользователей дают правильный ответ на эту арифметическую задачу. И это, я считаю, неплохо. А теперь на этом примере рассмотрим характерные ошибки, которые делают остальные 30％.

Наиболее существенная ошибка. Простой арифметический пример пытаются решить алгебраическими методами, в частности раскрывая скобки (об этом методе поговорим в дальнейшем), тем самым нарушая порядок действий. Сразу замечу, алгебра и арифметика – это две разные дисциплины. В арифметике, в отличие от алгебры, основная функция скобки – обозначение приоритета очерёдности действий. Каких только определений не придумывается для этого ошибочного решения: коэффициент скобки, действия на скобку и т. д. Если вы таким образом решите данный пример, то получите 2.5. Внимание: неправильное решение.

10: (2×4 – 2×2) =10: (8—4) = 10:4 = 2.5

Другие пользователи помнят, что сначала выполняется действие в скобках, но потом делает характерную ошибку: они умножают двойку на то, что получилось в скобках, а потом уже выполняют деление. Запомните, никакого приоритета умножение перед делением не имеет, поэтому все оставшиеся действия делаются слева направо в порядке их написания. Если вы сделаете ошибку такого рода получите снова 2.5. Внимание: неправильное решение.

10:2×2 = 10:4 = 2.5.

Я не представляю, какие дебаты могли возникнуть, если был бы выложен более сложный арифметический пример. Часть тех, что делают ошибку утверждают, что их так учили и 30—50 лет назад этот пример решался именно так. Замечу, что арифметика – древняя наука и те правила, которые сложились ещё много веков назад действуют и по сей день. Интересно, что те, кто правильно решает данный пример не настолько агрессивны, как те, что решают его неправильно. В чём природа такого явления нужно спросить у психологов. Ещё одно ошибочное утверждение, некоторые доказывают, что правильных ответов может быть два и более. Это заблуждение, арифметика – точная наука и у любого задания есть единственно верный ответ (в отличие, кстати, от алгебры).

О единственно верном ответе есть отличный видеоролик, снятый американскими кинематографистами. Впрочем, смысл этого ролика немного в другом, я попытаюсь пересказать его содержание, но рекомендую вам самим посмотреть его. Достаточно в поисковой строке набрать 2+2=22 или название ролика «Альтернативная математика». В начале учительница пытается объяснить мальчику, что два плюс два равняется четырём, а не 22, как тот написал в тесте. Беседа с ребёнком ничего не даёт и тогда учительница приглашает родителей мальчика. Родители в недоумении и заявляют, что учитель не имеет права навязывать школьнику своё мнение, если ребёнок считает что два плюс два равняется 22, значит нужно согласится с его мнением. Дальше история становится ещё абсурдней. Директор школы настаивает на том, чтобы учительница извинилась перед родителями, т.к своим поведением она мешает школьникам мыслить самостоятельно и навязывает свои догмы. Дальше – больше, перед образовательным учреждением ученики выходят с плакатами на площадь, а учительницу вызывают на комиссию с требованием признать, что существует несколько правильных ответов. Учительница возражает: «Есть только один правильный ответ». В конце-концов учительница отстаивает свою точку зрения. Директор вызывает учительницу и перед журналистами и телевизионщиками говорит: « Нам придётся вас уволить, вы получите 4000. 2.000 за прошлый месяц и 2.000 за текущий. И тут учительница иронично замечает: « Не верно, это 22000». На этом ролик заканчивается. На самом деле он не о том что, математика – точная наука, здесь больше критика в сторону толерантного образования США. На самом деле создатели ролика немного ошиблись, т.к 2000 +2000 = 2 000 2 000,т.е 20 миллионов 2 тысячи, если считать по правилам альтернативной математики.