Ю. Щербакова - Начертательная геометрия: конспект лекций
- Название:Начертательная геометрия: конспект лекций
- Автор:
- Жанр:
- Издательство:Конспекты, шпаргалки, учебники «ЭКСМО»b4455b31-6e46-102c-b0cc-edc40df1930e
- Год:2007
- Город:Москва
- ISBN:5-699-19332-4
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Ю. Щербакова - Начертательная геометрия: конспект лекций краткое содержание
Данное учебное пособие представляет собой курс лекций и предназначено для студентов, сдающих экзамен по специальности «Начертательная геометрия».
Подготовлено с учетом требований Министерства образования РФ.
Начертательная геометрия: конспект лекций - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Если проставить буквы в вершинах параллелепипеда, то две проекции уже будут его определять (рис. 89).
Если не проставлять буквы в вершинах параллелепипеда, то только три проекции определят его форму (рис. 89). Чтобы убедиться в этом, начертим две из этих проекций (фронтальную и профильную) (рис. 90) и попытаемся построить третью – горизонтальную.
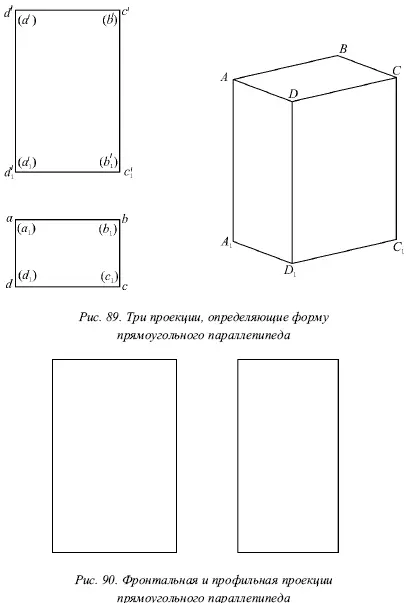
Анализируя эти две проекции, можно представить себе не одну, а несколько различных проекций горизонтальной грани. Поэтому, кроме исходного прямоугольного параллелепипеда, еще несколько тел будет иметь данные две проекции и отличаться только третьими.
Лекция № 8. Определение натуральных величин
1. Вращение точки около оси, перпендикулярной плоскости проекций
На рисунке 91 дана ось вращения I , которая перпендикулярна горизонтальной плоскости, и произвольно расположенная в пространстве точка А . При вращении около оси I эта точка описывает окружность, плоскость которой перпендикулярна оси I . А отсюда следует, что она параллельна горизонтальной плоскости, поэтому на горизонтальную плоскость эта окружность А проецируется без искажения.
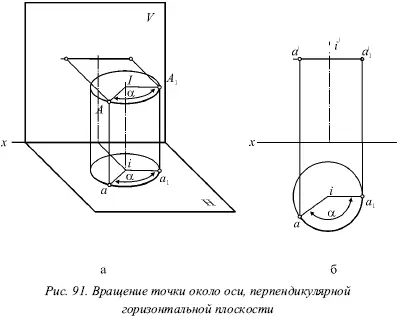
Обратим внимание на то, что H – это горизонтальная плоскость, а V – фронтальная плоскость.
Пусть точка А повернется около оси вращения на некоторый угол. Она перейдет в положение А 1, при этом ее горизонтальная проекция а пройдет такой же путь около следа оси вращения и повернется на тот же угол. На плоскости V фронтальная проекция а́ будет перемещаться по прямой, которая параллельна оси х .
На рисунке 92 показана ось вращения I , перпендикулярная фронтальной плоскости. Можно сказать, что в этом случае горизонтальная и фронтальная плоскости поменялись ролями. Окружность здесь представляет траекторию точки В . При этом вращении она проецируется без искажения на фронтальную плоскость. На горизонтальной плоскости ее проекция b перемещается по прямой, параллельной оси х .
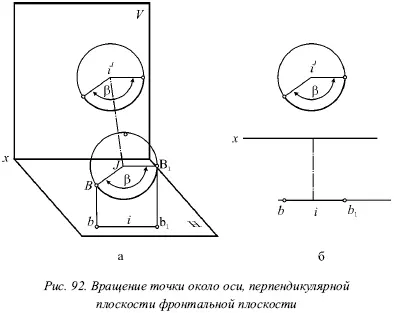
2. Определение натуральной величины отрезка путем вращения
Отрезок, параллельный какой-нибудь плоскости проекций, проецируется на нее без искажения. Если повернуть отрезок таким образом, чтобы он стал параллельным одной из плоскостей проекций, то можно определить его натуральные размеры. Это вращение осуществляется легче всего вокруг оси, которая перпендикулярна одной из плоскостей проекций.
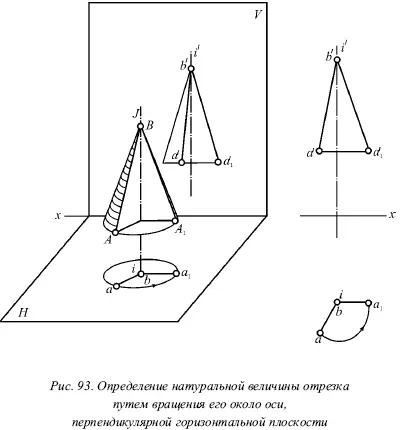
На рисунке 93 показано вращение отрезка около оси, которая перпендикулярна горизонтальной плоскости. Пусть дан произвольный отрезок АВ , тогда проведем через точку В вертикальную прямую I . Она, в свою очередь, перпендикулярна горизонтальной плоскости. Теперь будем вращать отрезок АВ около этой прямой I . При этом отрезок АВ опишет поверхность прямого кругового конуса, а его вершина будет расположена в точке В (рис. 93). Прямая I здесь является осью конуса. В этом случае точка А описывает окружность, которая является основанием этого конуса. Данное основание изображается в натуральную величину на горизонтальной плоскости, в виде отрезка, параллельного оси х , на фронтальной плоскости. Отрезок АВ представляет собой образующую конуса.
Отрезок АВ будем вращать до тех пор, пока он не расположится параллельно фронтальной плоскости (таких положений будет два, и они совпадают на фронтальной плоскости с контуром вспомогательного конуса). В этом случае его горизонтальная проекция должна стать параллельной оси х . Оказалось, что точка В легла на ось вращения, поэтому при вращении отрезка она не изменит своего положения. На рисунке 93 показано, как горизонтальная проекция а описывает дугу окружности с центром в точке b , а фронтальная проекция а перемещается по прямой, параллельной оси х.
Проекция является натуральным изображением отрезка АВ , т. е. á 1 b́ = AB .
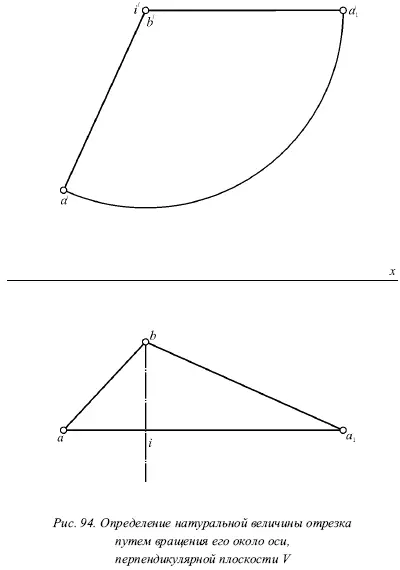
На рисунке 94 показано вращение отрезка около оси, которая перпендикулярна фронтальной плоскости. При этом натуральная величина отрезка АВ установлена вращением около оси I , которая проходит через точку В перпендикулярно фронтальной плоскости. В этом случае построение абсолютно аналогично тому, которое было рассмотрено ранее.
Лекция № 9. Пересечение поверхности многогранника проецирующей плоскостью
1. Общие понятия
Если пересечь поверхность многогранника плоскостью, то в сечении получается многоугольник. Первая задача заключается в построении проекций многоугольника, получившегося в сечении, затем следует определить натуральный вид этого многоугольника. Также необходимо построить развертку поверхности данного многогранника, причем нужно указать на его поверхности след секущей плоскости.
Построение проекций фигуры сечения можно выполнить двояко.
1. Можно найти точки встречи ребер многогранника с секущей плоскостью, после чего соединить проекции найденных точек. В результате этого получатся проекции искомого многоугольника. В этом случае целью задачи является определение точек встречи нескольких прямых с данной плоскостью.
2. Построение можно выполнить по-другому: последовательно найти линии пересечения каждой из граней многогранника с секущей плоскостью, тогда придется несколько раз строить линию пересечения двух плоскостей.
Чтобы определить истинные размеры многоугольника, который получается в секущей плоскости, обычно поступают следующим образом: совмещают эту плоскость с плоскостью проекций.
Плоская фигура, которая получается, если все грани вычертить в настоящую величину на плоскости чертежа в том порядке, в каком они следуют на самом многограннике, называется разверткой(или выкройкой) поверхности данного многогранника. Для ясности можно сказать, что поверхность многогранника как бы разрезается вдоль некоторых его ребер так, чтобы потом эту поверхность можно было совместить с плоскостью чертежа. В том случае если поверхность многогранника пересечена некоторой плоскостью, тогда для построения развертки на каждой грани следует изобразить след секущей плоскости.
Читать дальшеИнтервал:
Закладка:










