Ю. Щербакова - Начертательная геометрия: конспект лекций

Построение развертки боковой поверхности многогранника осуществляется в два основных этапа:

1) определением истинных размеров всех элементов каждой ее грани. Именно благодаря им можно построить изображение этой поверхности в натуральную величину;

2) последовательное построение каждой грани в натуральную величину исходя из найденных раньше элементов.

В случае если данная грань многогранника представляет собой треугольник, тогда, чтобы построить ее в натуральную величину, нужно просто знать размеры всех ее сторон. Если грань многогранника представляет собой четырехугольник, то, кроме четырех его сторон, следует знать еще какой-либо ее элемент (или один из углов, или диагональ и т. п.). В некоторых случаях вспомогательными линиями могут быть следы секущей плоскости.

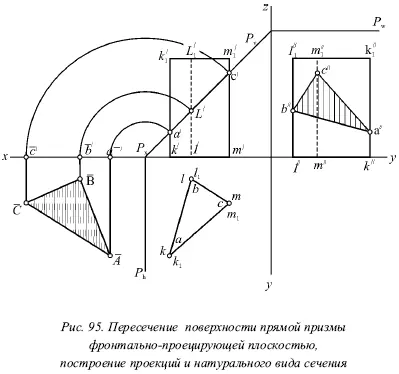
На рисунке 95 показано пересечение поверхности прямой призмы фронтально-проецирующей плоскостью Р . Первым делом нужно рассмотреть проекции сечения. Ребра призмы перпендикулярны горизонтальной плоскости и проецируются на ней точками. Здесь горизонтальная проекция а точки А является пересечением ребра KK 1с плоскостью Р , она совпадает с проекцией k . Фронтальная проекция а располагается на следе Р v. Следовательно, горизонтальная проекция áb́ć искомого сечения совпадает с проекцией основания klm . При этом фронтальная проекция аbс расположена на следе Р v. Если располагать двумя проекциями и сечениями, то нетрудно построить третью.

Для определения истинных размеров треугольника ABC нужно совместить плоскость Р с горизонтальной плоскостью путем вращения около горизонтального следа P h.

Чтобы построить развертку, надо иметь все необходимые элементы на эпюре, основание проектируется без искажения на горизонтальную плоскость, а все ребра с точками пересечения – на фронтальную плоскость.

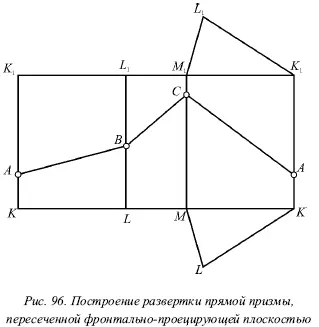
Начинать построение развертки следует с ребра КК 1, поместив его где-нибудь в стороне. На рисунке 96 показаны вспомогательные прямые, проведенные перпендикулярно ребру КК 1. После этого от точки К вправо откладывается отрезок KL , равный стороне основания k l. Затем проводят второе ребро LL 1, завершая построение натурального изображения грани KK 1 LL 1. Далее справа от этой грани строят натуральное изображение следующей грани LL 1 M 1 M и продолжают до тех пор, пока не будет целиком построена развертка боковой поверхности призмы.

После этих действий на всех ребрах отмечают точки А, В и С , откладывая на развертке KA = ḱá, LB = ĺb́ и МС = ḿс́ .

Отметим, что на развертке отрезки АВ, ВС и СА имеют натуральные размераы сторон треугольника сечения, который показан на чертеже слева в натуральную величину (треугольник ABC ). В связи с этим данные отрезки должны быть равны соответствующим сторонам треугольника. Проверкой точности построения является равенство этих отрезков на чертеже.

Теперь осталось только пристроить к развертке боковой поверхности призмы верхнее и нижнее основания, т. е. два треугольника MKL и M 1 K 1 L 1. При этом каждый из треугольников строится по трем сторонам.

На рисунке 97 показано пересечение поверхности призмы горизонтально-проецирующей плоскостью Q . Здесь сечением является прямоугольник АА 1 В 1 В , одна пара сторон которого АВ и A 1 B 1проецируется без искажения на горизонтальную плоскость, а вторая пара AA 1и ВВ 1– на фронтальную и профильную плоскости.

Пусть натуральные размеры обеих сторон прямоугольника АА 1 В 1 В даны, но в разных местах. Для построения прямоугольника в натуральную величину нужно через а и b провести прямые перпендикулярно q , затем наметить на них где-нибудь положение точек А и В ( AB ⊥ aA ). После этого откладываются от точек А к В на вспомогательных линиях натуральные размеры сторон АА 1и ВВ 1, при этом их берут с фронтальной проекции.

Строя натуральную величину сечения, мы как бы совместили прямоугольник с горизонтальной плоскостью, вращая его около горизонтального следа АВ ( АВ = аb ). После чего для удобства немного отодвинули это изображение от линии q .

Построение натурального вида прямоугольника

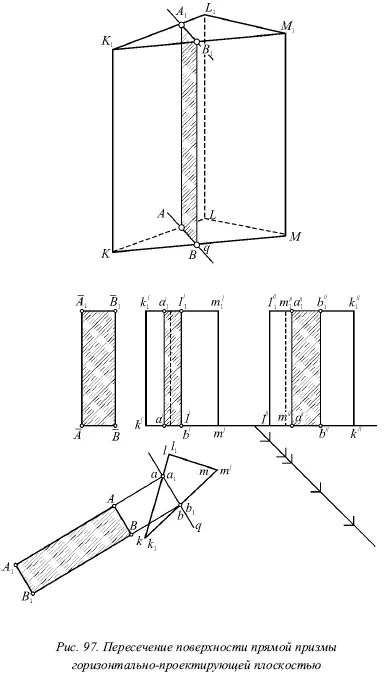
сечения весьма удобно делать слева от фронтальной проекции призмы (прямоугольник ABB 1 A 1).

На рисунке 98 показано пересечение поверхности пирамиды фронтально-проектирующей плоскостью Р . На рисунке 98б изображена фронтальная проекция а точки встречи ребра KS с плоскостью P . Она определяется пересечением следа P vс фронтальной проекцией ребра ḱś (рис. 98 а). Если фронтальная проекция а́ точки А дана, то легко найти её горизонтальную проекцию а .

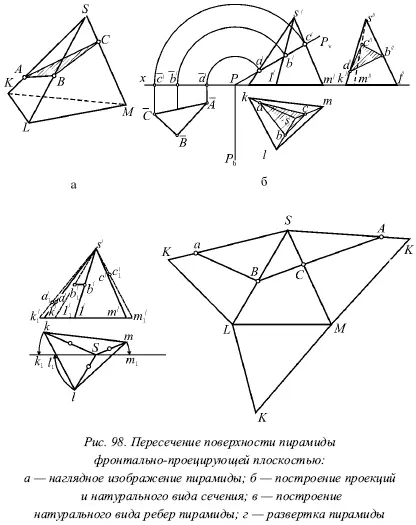
На рисунке 98, б показаны натуральные размеры ABC сечения ABC , которые были определены совмещением его с горизонтальной плоскостью путем вращения около следа P h. Отдельно на этом рисунке показаны элементы, которые необходимы для построения развертки. Натуральные размеры ребер пирамиды можно найти путём вращения их около оси, проходящей через вершину S перпендикулярно горизонтальной плоскости, как показано на рисунке 98 в. На рисунке 98 г показана развертка, а изображение каждого из треугольников, входящих в состав развертки, можно построить по трём его сторонам – ребрам.

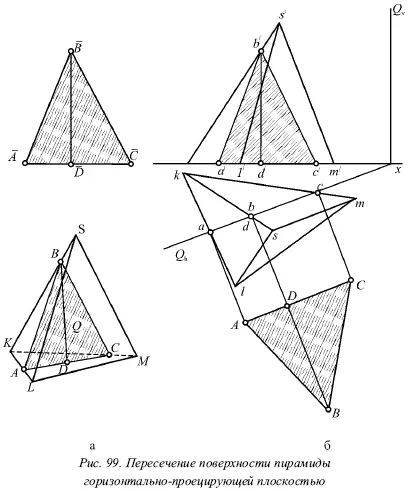
На рисунке 99 показано пересечение поверхности пирамиды горизонтально-проецирующей плоскостью Q . Треугольник ABC является сечением поверхности пирамиды плоскостью Q , основание АС которого проецируется на горизонтальную плоскость без искажения, а высота BD – на фронтальную и профильную плоскости.

Чтобы построить натуральное изображение сечения, нужно провести через проекции а, с и d вспомогательные прямые, которые перпендикулярны Q h. После этого следует провести прямую АС параллельно Q h( AC ⊥ аА ), точка D будет лежать на АС . Затем необходимо отложить от точки D на прямой Dd высоту треугольника ( DB = d́b́ ). Это определит положение вершины В . Теперь треугольник ABC представляет собой натуральный вид сечения поверхности данной пирамиды плоскостью Q . Строить натуральный вид треугольника сечения весьма удобно слева от фронтальной проекции (треугольник ABC ).