Питер Эткинз - Десять великих идей науки. Как устроен наш мир.

Есть множество других весьма причудливых свойств простых чисел. Например, обладавший необычайным воображением польско-американский математик Станислав Улам (1909-84) обнаружил, что, если вы запишете все натуральные числа по спирали, так что 1 окажется в центре, 2 справа, 3 над 2, 4 над 1, 5 слева от 4 и так далее, и пометите все простые числа, то они будут иметь тенденцию попадать на диагональные линии (рис. 10.3). Улам использовал свое воображение и другими способами: вместе с Эдвардом Теллером он открыл, как инициировать взрыв водородной бомбы.

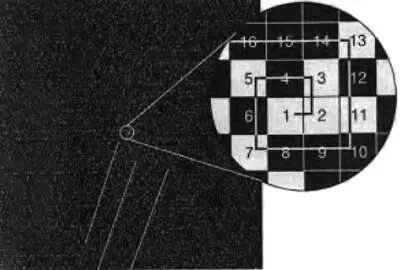
Рис. 10.3.Спираль Улама. Если записать все натуральные числа по спирали, как показано на вставке, и пометить простые числа, то они проявят тенденцию располагаться на диагональных прямых, как можно видеть, рассматривая черную зону с простыми числами, изображенными, подобно звездам, белыми точками. Мы нарисовали некоторые из диагоналей, чтобы показать их положение; вы могли бы различить и другие.

Хотя простые числа являются фундаментальными атомами умножения (так же, как 1 тривиально является фундаментальным атомом сложения), они, может быть, играют фундаментальную роль и в сложении тоже. В 1742 г. Кристиан Гольдбах (1690-1764), однажды оказавшийся учителем царя Петра II, в письме к прославленному математику Леонарду Эйлеру (1707-83) предположил, что каждое четное натуральное число, большее 2, является суммой двух простых чисел. Так, мы имеем 2 + 2 = 4, 3 + 3 = 6, 3 + 5 = 8, …, 47 + 53 = 100, …. Гипотеза Гольдбаха до сих пор не доказана, несмотря на приложение огромных усилий. Трудность, по-видимому, связана с тем фактом, что простые числа, произошедшие из концепции умножения, помещаются здесь в контекст сложения. Однако эта гипотеза может быть примером того, что постепенно выдвигается в центр сцены: она, возможно, не может быть доказана и поэтому, в некотором смысле, эта гипотеза может быть ни истинной, ни ложной. Гольдбах предположил также, что каждое нечетное натуральное число является суммой трех простых чисел. Это предположение частично доказал — доказательство справедливо лишь для больших чисел — в 1937 г. русский математик Иван Матвеевич Виноградов (1891-1983).

Деление одного натурального числа на другое также вводит новый класс чисел, называемых рациональными числами (от «рацио»; заслуживающее доверия качество таких чисел отражено в нашем привычно используемом термине «рациональный», обозначающем разумность, основанность на разуме); примеры между 0 и 1 включают 1/2 = 0,500 000 000… и 3/7 = 0,428 571 428 57…. Заметим, что десятичные формы рациональных чисел содержат либо бесконечно повторяющийся 0, либо бесконечно повторяющуюся конечную последовательность чисел.

Если вы начнете думать как математик, который идет дальше непосредственно воспринимаемого, ищет обобщений и исследует, куда они ведут, то вы почувствуете зуд от шевелящегося в вас вопроса: существуют ли числа, не содержащие повторяющихся последовательностей и поэтому не выражаемые в виде отношения натуральных чисел? Существование таких иррациональных чисел было впервые обнаружено пифагорейцами, чья целостная философия жизни в Кротоне (сегодня Кротон, находящийся в каблуке Италии, носит название Кротоне), основанная на гармонии рациональных чисел, запрете мочиться в сторону Солнца или чистить ногти во время жертвоприношения и на поддержании социального мира путем исключения из пищи бобов (практиковавшегося самим Пифагором, чему он обучился у египетских жрецов, среди которых однажды жил) [49], была ниспровергнута, когда обнаружилось, что квадратный корень из 2, √2, = 1,414 213 5… является иррациональным и не может быть получен с помощью деления одного натурального числа на другое. С тех пор многие другие числа были идентифицированы как иррациональные, среди них π = 3,141 59… (отношение окружности к диаметру круга, π введено в качестве символа Эйлером в 1737 г., а иррациональность была установлена в 1767 г.) [50], π 2 (иррациональность установлена в 1794 г.) и e = 2,718 28… (основание натурального логарифма). Иррациональность доказать трудно: например, хотя известно, что е π иррационально, все еще неизвестно, обладает ли этим свойством π e .

Рациональные и иррациональные числа, как положительные, так и отрицательные, включая ноль, называются действительными числами . Чтобы вообразить действительные числа, мы можем представить себе, что каждое число соответствует точке прямой, где самые большие числа находятся справа. Действительные числа, подобно точкам на прямой, простираются от минус бесконечности слева до плюс бесконечности справа и включают все возможные числа — целые, рациональные и иррациональные. Это соответствие действительных чисел с точками прямой явилась решающим шагом в осознании того, что геометрия — свойства различных линий, а значит, наборов точек, а значит, наборов действительных чисел — может рассматриваться, как ветвь арифметики. Мы не пойдем по этому пути в настоящей главе, но вам следует иметь в виду, что, хотя мы и будем сосредотачиваться на идеях, которые являются явно арифметическими, в скрытом виде они включают и другие области математики, такие как геометрия (рис. 10.4).

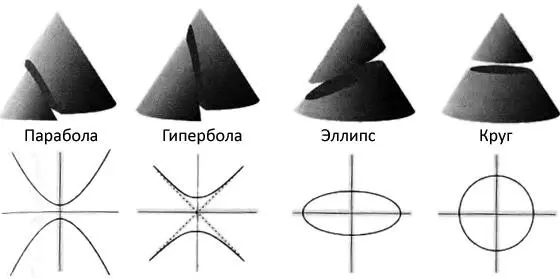
Рис. 10.4.У греков было абстрактное представление о пространстве, и поэтому они преуспели в геометрии. Здесь мы видим, как параболы, гиперболы и эллипсы (включая частный случай круга) можно рассматривать как наборы чисел, получаемые посредством сечений конуса в разных направлениях. Теперь мы знаем, благодаря пионерской работе Декарта, как связать эти формы с алгебраическими уравнениями, и поэтому можем видеть связи между геометрией пространства и арифметическими свойствами определенных наборов чисел.

На самом деле, арифметика даже более богата. В соответствии с чрезвычайно важной, но обманчиво краткой теоремой, которую доказал в 1915 г. немецкий математик Леопольд Лёвенгейм (1878-1957) и усовершенствовал в 1920 г. норвежец Альберт Тораф Сколем (1887-1963), система правил, подобных правилам арифметики, действует в любой области знания, которая может быть формализована в терминах набора аксиом. Если бы в школе вам говорили, что, согласно теореме Лёвенгейма-Сколема , вы, на самом деле, моделируете процесс вывода заключений из квантовой механики, теории естественного отбора и юриспруденции (постольку, поскольку эти области знания могут быть выражены в терминах аксиом), это могло бы смягчить утомление от узнавания, как извлекать квадратный корень и проделывать длинные упражнения на деление. То же самое верно относительно остальной части этой главы: хотя многое в ней будет читаться, как относящееся к арифметике, имейте в виду, что это в действительности относится к любой систематизированной области человеческого знания . Если уж это не захватывает дух, то я просто не знаю, чем вас пронять.