Питер Эткинз - Десять великих идей науки. Как устроен наш мир.
- Название:Десять великих идей науки. Как устроен наш мир.
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:978-5-17-051198-3, 978-5-17-050272-1, 978-5-271-19820-5, 978-5-271-19821-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Питер Эткинз - Десять великих идей науки. Как устроен наш мир. краткое содержание
Эта книга предназначена для широкого круга читателей, желающих узнать больше об окружающем нас мире и о самих себе. Автор, известный ученый и популяризатор науки, с необычайной ясностью и глубиной объясняет устройство Вселенной, тайны квантового мира и генетики, эволюцию жизни и показывает важность математики для познания всей природы и человеческого разума в частности.
Десять великих идей науки. Как устроен наш мир. - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Чтобы убедиться в том, что это так, взгляните на рис. 10.6, где я нарисовал таблицу всех рациональных чисел (но показал только малую часть из них). Поверху вправо идут натуральные числа, указывающие числитель дроби, которую мы намереваемся построить, а слева вниз идут натуральные числа, указывающие ее знаменатель. Внутренняя часть таблицы содержит все возможные дроби, получаемые делением одного натурального числа на другое. Здесь будет много повторений, таких как 3/6 и 4/8 оба равны 1/2, но это не имеет значения. Теперь мы можем провести линию, которая пробегает от первой цифры таблицы через все остальные, как показано на рис. 10.6. Затем, продвигаясь вдоль этой линии, будем вести счет 1, 2, … каждой встречающейся дроби. Таким способом все дроби — все рациональные числа — оказываются поставленными во взаимно однозначное соответствие с натуральными числами. Мы никогда не выйдем за пределы натуральных чисел, поэтому количество рациональных чисел таково же, как и количество натуральных чисел, несмотря на то, что они расположены плотнее, чем натуральные числа. Существует бесконечное число рациональных чисел между 0 и 1 и между 1 и 2, но их бесконечное число между 1 и 2 такое же! Короче говоря, мы всегда можем пересчитать рациональные числа — мы говорим, что они счетны — и получить ответ «бесконечность» безотносительно к интервалу чисел, на котором производится счет. Возможно, вы начинаете понимать, что бесконечность является расплывающимся и ускользающим понятием.
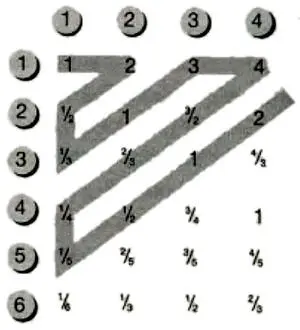
Рис. 10.6.Рациональные числа можно поставить в соответствие с натуральными числами, поэтому они являются счетными. В верхнем ряду находятся натуральные числа, указывающие числитель дроби p/q, а слева вниз идут натуральные числа, указывающие ее знаменатель. Продвигаясь по извилистой диагональной линии, мы можем пересчитать рациональные числа (включая их многочисленные повторения).
Алгебраические числа — числа, являющиеся решениями алгебраических уравнений — тоже являются счетными. Вы можете ухватить идею доказательства этого утверждения, заметив, что каждое алгебраическое уравнение состоит из степеней x (выражений, подобных x 3 ), умноженных на целое число (как в 4x 3+ 2x − 1 = 0 ). Поэтому существует взаимно однозначное соответствие между решениями уравнений — алгебраическими числами — и целыми числами, определяющими уравнения. Мы можем заключить, что алгебраические числа являются счетными и, хотя их число бесконечно, мощность их такая же, как у натуральных чисел.
А сколько же иррациональных чисел, чисел, которые не могут быть выражены как отношения натуральных чисел? Возможно, вы думаете, что их тоже бесконечное число. Вы, вероятно, правы. Но то, чего вы, вероятно, не знаете (если вы, конечно, не знали ответ заранее), это то, что иррациональные числа более бесконечны, чем натуральные. То есть иррациональные числа имеют большую мощность, чем натуральные числа: их количество более бесконечно. Красивую аргументацию, впервые выявившую эту странную черту, предложил космополит от рождения Георг Фердинанд Людвиг Филлип Кантор (1845-1918), рожденный от датчанина и русской в Санкт-Петербурге, но проживший большую часть жизни в Германии. Его жизнь была полна разочарований, главным образом потому, что он работал на переднем крае современной ему математики и внес в поле рассмотрения бесконечность. Отчасти в результате стресса, создаваемого неприятием его работы со стороны консервативной части математического истеблишмента, в частности, влиятельного Леопольда Кронекера (1823-91), который был предубежден против всех разновидностей чисел, кроме рациональных, Кантор начал страдать серьезным умственным расстройством, все более обращаясь к религии, ибо он считал, что бесконечные множества объектов, которые он рассматривает, существуют как реализованные сущности разума Бога, и что он, Кантор, есть сосуд, избранный для того, чтобы явить их, некто вроде математического Иоанна Крестителя. Между приступами своей навязчивой идеи о том, что автором Шекспира был Бэкон, Кантор проводил все более длительные периоды в психиатрических клиниках, исследуя пограничные области религии, такие как масонство, теософия и учение розенкрейцеров, в точности так же, как он исследовал пограничные области математики, но с меньшим результатом. Определенно рискуют стать безумными те, кто всматривается в бездну бесконечности, что, возможно, начнете понимать и вы по мере развертывания этой главы.
В 1874 г. Кантор обнаружил простой аргумент, показывающий, что иррациональные числа более многочисленны, чем рациональные. Мы будем использовать этот аргумент и его видоизменения в других контекстах, поэтому стоит на нем задержаться. Начнем выписывать список случайно выбранных чисел, лежащих между 0 и 1, и последовательно их пронумеровывать (в левой колонке):
| 1 | 0, 198 402 957 820… |
| 2 | 0,4 38 291 057 381… |
| 3 | 0,68 4930 175 839… |
| 4 | 0,782 948 261 859… |
| 5 | 0,500 0 00 000 000… |
| 6 | 0,483 91 3562 785… |
| … |
Теперь покажем, что каким бы длинным ни был список, включая бесконечную длину, существуют числа, которых в нем нет. Чтобы проделать это, построим новое число, выбирая первую цифру после десятичной точки в первом числе списка, вторую во втором числе и так далее и записывая в новом числе на соответствующем месте другую цифру, замена жирных цифр, например, даст нам новое число 0,134 903…. Этого числа определенно нет в списке, поскольку оно отличается от первого числа, оно отличается от второго числа и так далее. Отсюда следует, что количество действительных чисел (рациональные вместе с иррациональными) больше, чем количество натуральных чисел, потому что, как бы ни был длинен список, мы всегда можем построить число, которого в нем нет. Мы говорим, что действительные числа несчетны .
Давайте посмотрим на это заключение немного более пристально. Мы только что видели, что действительные числа (натуральные числа плюс рациональные числа и иррациональные числа) являются несчетными. Однако мы видели, что натуральные числа, рациональные числа и алгебраические числа все счетны. Мы можем сделать вывод, что числа, которые делают действительные числа несчетными, все являются трансцендентными (такими, как π и e) .
Сделаем паузу, чтобы осознать значение этого необычного вывода. Он означает, что огромное большинство чисел — на самом деле, бесконечно преобладающее большинство — являются трансцендентными. Это весьма удивительно, особенно потому, что трансцендентные числа гораздо менее нам знакомы, чем «обычные» числа, и вы даже могли никогда о них раньше не слышать. Тот факт, что трансцендентные числа в преобладающей степени более многочисленны, чем другие виды чисел, явился основанием для моего замечания в начале главы, что удивительным является то, что мы вообще можем считать: натуральные числа крайне редко распределены среди действительных чисел, и каждое из них окружено бесконечностью трансцендентных чисел. Эдвард Темпл Белл выразил это графически, когда написал
Читать дальшеИнтервал:
Закладка: