Морис Клайн - Математика. Утрата определенности.

Представление о математике как о своде априорных истин было созвучно умонастроениям математиков. Но большинство из них не обратило внимания на то, каким образом Кант пришел к своим заключениям. По теории Канта, все утверждения математики не являются неотъемлемыми признаками физического мира, а создаются человеческим разумом. Такой вывод должен был бы насторожить математиков. Откуда известно, что разум всех людей устроен так, что организует ощущения совершенно одинаково и что организация пространственных ощущений непременно должна быть евклидовой? Какие мы имеем основания это утверждать? В отличие от Канта математики и физики продолжали верить во внешний мир, подчиняющийся законам, не зависящимот человеческого разума. Мир устроен рационально, считали они, и человек лишь раскрывает план, лежащий в основе мироздания, а далее, пользуясь этим планом, пытается предсказывать то, что происходит во внешнем мире.

Философия Канта и его авторитет раскрепостили и одновременно ограничили научно-философскую мысль. Подчеркивая силу разума как организующего начала в упорядочении чувственного опыта о мире, который нам не дано узнать доподлинно, Кант проложил путь к новым представлениям, в корне противоположным тем, которые в его время считались твердо установленными. Но упорно подчеркивая, что наш разум с необходимостью организует пространственные ощущения в соответствии с законами евклидовой геометрии, Кант тем самым тормозил формирование иных взглядов. {43}Если бы Кант с большим вниманием следил за тем, как развивались события в современной ему математике, то, возможно, он не стал бы настаивать на том, что упорядочивание пространственных ощущений по образу и подобию евклидовой геометрии является единственным, которое может допустить наш разум.

Безразличие к богу и даже лишение его роли творца законов мироздания, а также кантианские взгляды на эти законы как якобы присущие самой природе человеческого разума «вызвали реакцию» со стороны творца всего сущего. Бог решил наказать кантианцев, и особенно этих самодовольных, погрязших в гордыне и чрезмерно самоуверенных математиков, и «подбросил» им неевклидову геометрию, возникновение которой нанесло сокрушительный удар по достижениям человеческого разума, всемогущего и, казалось бы, не нуждающегося ни в чьей помощи.

Хотя к началу XIX в. роль бога становилась все менее ощутимой и некоторые радикально настроенные философы, например Юм, отрицали все истины, математики того времени по-прежнему продолжали верить в истинность собственно математики и математических законов природы. Евклидова геометрия была наиболее почитаемым разделом математики не только потому, что именно с нее началось дедуктивное построение математических дисциплин, но и по той причине, что ее теоремы, как было установлено на протяжении более двух тысячелетий, полностью соответствовали результатам физических исследований. И именно евклидову геометрию «бог» избрал объектом нападения.

Одна из аксиом евклидовой геометрии издавна беспокоила математиков, однако совсем не потому, что они сомневались в ее истинности. Сомнения вызывала у них лишь формулировка аксиомы. Мы имеем в виду аксиому о параллельных, или, как ее часто называют, пятый постулат Евклида. Сам Евклид сформулировал пятый постулат следующим образом:

Если прямая, падающая на две прямые [рис. 4.1], образует внутренние и по одну сторону углы, меньшие двух прямых, то продолженные эти две прямые неограниченно встретятся с той стороны, где углы меньше двух прямых.

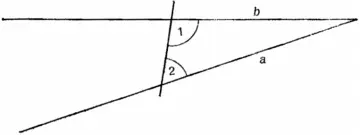
Рис. 4.1.Пятый постулат Евклида.

Иначе говоря, если углы 1 и 2 в сумме меньше 180°, то прямые а и b, продолженные достаточно далеко, пересекутся.

У Евклида были веские основания сформулировать аксиому о параллельных именно так, а не иначе. Он мог бы утверждать, например, что если сумма углов 1 и 2 равна 180°, то прямые а и b параллельны. Но Евклид явно боялся предположить, что могут существовать бесконечные прямые, которые никогда не пересекаются: любое утверждение о бесконечных прямых не подкреплялось опытом, в то время как аксиомы по определению должны были быть самоочевидными истинами о физическом мире. Но опираясь на свою аксиому о параллельных и другие аксиомы, Евклид доказал существование параллельных.

Математики считали, что аксиома о параллельных в том виде, как ее сформулировал Евклид, слишком сложна. Ей недоставало простоты других аксиом. Должно быть, и сам Евклид был недоволен своим вариантом аксиомы о параллельных, ибо обратился к ней, лишь доказав все теоремы, какие только смог вывести без ее использования.

Со временем стала жизненно важной сходная проблема, над которой поначалу задумывались лишь немногие. Она сводилась к вопросу о том, существуют ли в физическом пространстве бесконечные прямые. Евклид достаточно осторожно постулировал лишь, что конечный отрезок прямой можно продолжить сколь угодно далеко, — но ведь даже и продолженный отрезок все равно оставался конечным. Тем не менее из рассуждений Евклида следовало, что бесконечные прямые существуют: если бы прямые были конечными, то их нельзя было бы продолжать сколь угодно далеко.

Первые попытки решить проблему, связанную с аксиомой Евклида о параллельных, были предприняты еще математиками Древней Греции. Эти попытки имели двоякую природу. Одни из них сводились к замене аксиомы о параллельных какой-нибудь более очевидной аксиомой. Другие были направлены на то, чтобы вывести аксиому о параллельных из девяти остальных аксиом Евклида: если бы удалось доказать, что пятый постулат Евклида в действительности представляет собой теорему, то все трудности отпали бы сами собой. На протяжении более двух тысячелетий многие десятки крупнейших математиков, не говоря уже о математиках меньшего ранга, безуспешно пытались решить проблему параллельных, предпринимая бессчетные попытки как первого, так и второго рода. История этой проблемы уходит корнями в глубокую древность и изобилует деталями, понятными лишь профессионалу. Мы опустим здесь ее потому, что ей посвящена обширная литература {44}, и, кроме того, этот вопрос не имеет прямого отношения к интересующей нас теме.

Из многих аксиом, предлагавшихся в качестве замены пятого постулата, упомянем лишь об одной. Ее и поныне приводят в некоторых учебниках геометрии. Этот вариант аксиомы о параллельных принадлежит Джону Плейферу (1748-1819), предложившему ее в 1795 г. (в английском «школьном» варианте «Начал» Евклида). Аксиома Плейфера гласит: существует одна и только одна прямая, проходящая через данную точку P, лежащую вне прямой l (рис. 4.2), в плоскости, задаваемой точкой P и прямой l , которая не пересекается с прямой l .