Джон Дербишир - Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.

Начинается все с «решета Эратосфена». Золотой Ключ по существу представляет собой способ, которым Леонард Эйлер сумел выразить решето Эратосфена в терминах анализа.

Эратосфен из Кирены (в настоящее время — городок Шаххат в Ливии) был одним из библиотекарей великой александрийской библиотеки. Около 230 года до P.X. — примерно через 70 лет после Эвклида — он разработал свой знаменитый метод решета для нахождения простых чисел.

Работает этот метод следующим образом. Сначала выпишем все целые числа, начиная с 2. Разумеется, нельзя выписать их все, поэтому остановимся на сотне с небольшим.

2 3 4 5 6 7 8 9 10 11

12 13 14 15 16 17 18 19 20 21

22 23 24 25 26 27 28 29 30 31

32 33 34 35 36 37 38 39 40 41

42 43 44 45 46 47 48 49 50 51

52 53 54 55 56 57 58 59 60 61

62 63 64 65 66 67 68 69 70 71

72 73 74 75 76 77 78 79 80 81

82 83 84 85 86 87 88 89 90 91

92 93 94 95 96 97 98 99 100 101

102 103 104 105 106 107 108 109 110 111

Теперь, начиная с 2 и сохраняя при этом саму двойку в неприкосновенности, уберем каждое второе число после 2.

2 3 . 5 . 7 . 9 . 11

. 13 . 15 . 17 . 19 . 21

. 23 . 25 . 27 . 29 . 31

. 33 . 35 . 37 . 39 . 41

. 43 . 45 . 47 . 49 . 51

. 53 . 55 . 57 . 59 . 61

. 63 . 65 . 67 . 69 . 71

. 73 . 75 . 77 . 79 . 81

. 83 . 85 . 87 . 89 . 91

. 93 . 95 . 97 . 99 . 101

. 103 . 105 . 107 . 109 . 111

Первое выжившее число после двойки — это 3. Сохраняя теперь 3 в неприкосновенности, удалим каждое третье число после 3, если оно еще не удалено. Получим

2 3 . 5 . 7 . . . 11

. 13 . . . 17 . 19 . .

. 23 . 25 . . . 29 . 31

. . . 35 . 37 . . . 41

. 43 . . . 47 . 49 . .

. 53 . 55 . . . 59 . 61

. . . 65 . 67 . . . 71

. 73 . . . 77 . 79 . .

. 83 . 85 . . . 89 . 91

. . . 95 . 97 . . . 101

. 103 . . . 107 . 109 . 111

Первое выжившее число после тройки — это 5. Сохраняя теперь 5 в неприкосновенности, удалим каждое пятое число после 5, если оно еще не удалено. Получим

2 3 . 5 . 7 . . . 11

. 13 . . . 17 . 19 . .

. 23 . . . . . 29 . 31

. . . . . 37 . . . 41

. 43 . . . 47 . 49 . .

. 53 . . . . . 59 . 61

. . . . . 67 . . . 71

. 73 . . . 77 . 79 . .

. 83 . . . . . 89 . 91

. . . . . 97 . . . 101

. 103 . . . 107 . 109 . 111

Первое выжившее число — это 7. Следующий шаг состоит в том, чтобы, сохраняя теперь 7 в неприкосновенности, удалить каждое седьмое число после 7, если его еще не удалили до этого. Первое число, которое выживает после этого, — 11. И так далее.

Если проводить эту процедуру бесконечно, то оставшимися числами будут все простые числа. В этом и состоит «решето Эратосфена». Если остановиться прямо перед тем, как пришло время обрабатывать простое число p — другими словами, прямо перед тем, как надо будет удалять каждое p- е число, если оно еще не было удалено, — то мы получим все простые числа, меньшие p 2. Поскольку выше мы остановились прямо перед обработкой семерки, у нас имеются все простые до 7 2, т.е. 49. После этого числа остаются и не простые числа, такие как 77.

Решето Эратосфена — вещь достаточно простая. И ему уже 2230 лет. Как же оно перенесет нас в середину XIX века, к глубоким результатам в теории функций? А вот как.

Я собираюсь повторить только что проведенную процедуру. (Именно по этой причине мы разобрали ее столь тщательно.) Но на этот раз я применю ее к дзета-функции Римана, которую мы определили в конце главы 5. Дзета-функция от некоторого аргумента s , большего единицы, записывается как

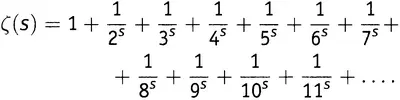
Стоит заметить, что такая форма записи предполагает выписывание всех положительных целых чисел — в точности как в начале наших действий с решетом Эратосфена (с тем только исключением, что на сей раз включена 1).

Сделаем такое: умножим обе части равенства на 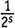. Получим

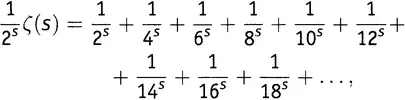
где мы пользовались 7-м правилом действий со степенями (которое говорит, например, что 2 s умножить на 7 s равно 14 s ). А теперь вычтем второе из этих выражений из первого. В одну из левых частей входит ζ(s) с множителем 1, а в другую — та же ζ(s) с множителем 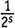. Вычитая, получаем

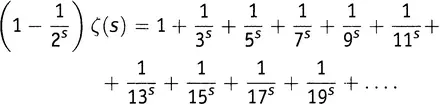
Вычитание устранило из бесконечной суммы все члены с четными числами. Остались только члены, в которые входят нечетные числа.

Вспоминая решето Эратосфена, умножим теперь обе части порченного равенства на 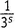, руководствуясь тем, что 3 — это первое выжившее число в правой части:

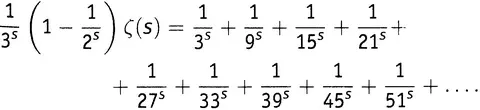
Теперь вычтем это выражение из того, которое мы получили ранее. При вычитании левых частей будем рассматривать 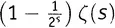как неделимую штуку, — просто как некоторое число (каковым оно, конечно, и является при любом заданном s ). Вся эта штука входит в левую часть одного выражения с множителем 1, а в левую часть другого — с множителем 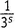. Вычитая, получаем

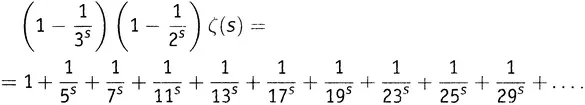
Из бесконечной суммы исчезли все члены, содержащие числа, кратные тройке! Первое выжившее число — это теперь 5.

Умножив теперь обе части полученной формулы на 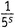, будем иметь

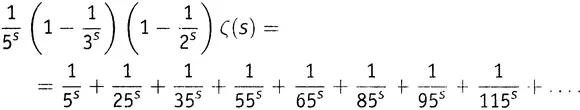
А теперь, вычитая это равенство из предыдущего и рассматривая на этот раз 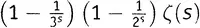как неделимую конструкцию, видим, что в левую часть одного выражения она входит с множителем 1, а в левую часть другого — с множителем 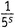. Вычитание дает