Джон Дербишир - Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.
- Название:Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.
- Автор:
- Жанр:
- Издательство:Астрель: CORPUS
- Год:2010
- Город:Москва
- ISBN:978-5-271-25422-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Джон Дербишир - Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике. краткое содержание
Сколько имеется простых чисел, не превышающих 20? Их восемь: 2, 3, 5, 7, 11, 13, 17 и 19. А сколько простых чисел, не превышающих миллиона? Миллиарда? Существует ли общая формула, которая могла бы избавить нас от прямого пересчета? Догадка, выдвинутая по этому поводу немецким математиком Бернхардом Риманом в 1859 году, для многих поколений ученых стала навязчивой идеей: изящная, интуитивно понятная и при этом совершенно недоказуемая, она остается одной из величайших нерешенных задач в современной математике. Неслучайно Математический Институт Клея включил гипотезу Римана в число семи «проблем тысячелетия», за решение каждой из которых установлена награда в один миллион долларов. Популярная и остроумная книга американского математика и публициста Джона Дербишира рассказывает о многочисленных попытках доказать (или опровергнуть) гипотезу Римана, предпринимавшихся за последние сто пятьдесят лет, а также о судьбах людей, одержимых этой задачей.
Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике. - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Позабудем на время о дзета-функции. Рассмотрим бесконечную сумму совсем другого типа:
S(x) = 1 + x + x 2+ x 3+ x 4+ x 5+ x 6 + ….
Сходится ли она вообще когда-нибудь? Без сомнения. Если x равно 1/ 2,то сумма представляет собой просто-напросто выражение 1.1из главы 1.iv, поскольку ( 1/ 2) 2= 1/ 4, ( 1/ 2) 3= 1/ 8и т.д. Следовательно, S ( 1/ 2) = 2, потому что именно к этому значению ряд и сходится. Более того, если вспомнить правило знаков, то (− 1/ 2) 2= 1/ 4, (− 1/ 2) 3= − 1/ 8и т.д., а следовательно, S (− 1/ 2) = 2/ 3согласно выражению 1.2из главы 1.v. Аналогичным образом выражение 1.3говорит нам, что S ( 1/ 3) = 1 1/ 2выражение 1.4— что S(− 1/ 3) = 1 3/ 4. Легко получить и еще одно значение для этой функции: S (0) = 1, поскольку нуль в квадрате, кубе и т.д. все равно равен нулю, и остается только единица, с которой ряд начинается.
Однако если x равен 1, то S (1) есть 1 + 1 + 1 + 1 + …, а этот ряд расходится. При x равном 2 расходимость еще более явная: 1 + 2 + 4 + 8 + 16 + …. Когда x равен −1, происходит странная вещь: по правилу знаков сумма принимает вид 1 − 1 + 1 − 1 + 1 − 1 + …. Такая сумма равна нулю, если взять четное число членов, и единице, если нечетное. Данное выражение определенно не убегает на бесконечность, но оно и не сходится. Математики рассматривают такое поведение как некоторый вид расходимости. Ситуация с x = −2 еще хуже: сумма 1 − 2 + 4 − 8 + 16 − … ведет себя так, словно убегает на бесконечность сразу по двум направлениям. Такая ситуация определенно далека от сходимости, и если вы скажете, что здесь налицо расходимость, то никто с вами спорить не будет.
Короче говоря, функция S(x) имеет значения, только когда x лежит в границах между −1 и 1, не включая сами границы. В других случаях у нее значений нет. В таблице 9.1 приведены значения функции S(x) для аргументов x между −1 и 1.
| x | S(x) |
|---|---|
| −1 или меньше | (нет значений) |
| −0,5 | 0,6666… |
| −0,333… | 0,75 |
| 0 | 1 |
| 0,333… | 1,5 |
| 0,5 | 2 |
| 1 или больше | (нет значений) |
Таблица 9.1.Значения функции S(x) = 1 + x + x 2+ x 3+ ….
Вот и все, что можно извлечь из бесконечной суммы. График этой функции показан на рисунке 9.1; на этом графике у функции нет вообще никаких значений к западу от −1 и к востоку от 1. Используя профессиональную терминологию, можно сказать, что область определения этой функции заключена строго между −1 и 1.
Рисунок 9.1.Функция S(x) = 1 + x + x 2+ x 3+ ….
Но смотрите, нашу сумму
S(x) = 1 + x + x 2+ x 3+ x 4+ x 5+ …
можно переписать в таком виде:
S(x) = 1 + x (1 + x + x 2+ x 3+ x 4+ …).
Ряд в скобках здесь равен просто S(x) : каждый член, встречающийся в одном, встречается также и в другом из двух выписанных выше рядов, а это и означает, что они совпадают.
Другими словами, S(x) = 1 + xS(x) . Перенося самый правый член в левую часть, получаем равенство S(x) − xS(x) = 1, или, другими словами, (1 − x ) S(x) = 1. Следовательно, S(x) = 1/(1 − x ). Возможно ли, чтобы за нашей бесконечной суммой скрывалась столь простая функция, как 1/(1 − x )? Может ли равенство
1/(1 − x ) = 1 + x + x 2+ x 3+ x 4+ x 5+ x 6+ … (9.2)
оказаться верным?
Без сомнения, может. Если, например, x = 1/ 2, то 1/(1 − x ) равняется 1/(1 − 1/ 2), что есть 2. Если x = 0, то 1/(1 − x ) равно 1/(1 − 0), что есть 1. Если x = − 1/ 2, то 1/(1 − x ) равняется 1/(1 − (− 1/ 2)), т.е. 1:1 1/ 2что есть 2/ 3. Если x = 1/ 3, то 1/(1 − x ) равняется 1/(1 − 1/ 3) т.е. 1: 2/ 3, что есть 1 1/ 2. Если x = − 1/ 3, то 1/(1 − x ) равняется 1/(1 − (− 1/ 3)), т.е. 1:1 1/ 3, что есть 3/ 4. Все сходится. Для аргументов − 1/ 2, − 1/ 3, 0, 1/ 3, 1/ 2, при которых мы знаем значения функции, значения бесконечного ряда S(x) такие же, как и значения функции 1/(1 − x ). Похоже, что этот ряд и эта функция — одно и то же.
Рисунок 9.2.Функция 1/(1 − x ).
Но они не одно и то же, поскольку у них различные области определения, как это видно из рисунков 9.1и 9.2. S(x) имеет значения только между −1 и 1, не включая границы; функция же 1/(1 − x ) имеет значения везде, за исключением точки x = 1. Если x = 2, то ее значение равно 1/(1 − 2), то есть −1. Если x = 10, то значение равно 1/(1 − 10), то есть − 1/ 9. Если x = −2, то значение равно 1/(1 − (−2)), то есть 1/ 3. Можно нарисовать график функции 1/(1 − x ). Как видно, он совпадает с предыдущим графиком в промежутке между −1 и 1, но имеет еще и значения к западу от −1 (включая саму −1) и к востоку от 1.
Мораль здесь в том, что бесконечный ряд может определять только часть функции; или, используя подобающие математические термины, бесконечный ряд может определять функцию только на части ее области определения. Остальная часть функции может где-то прятаться, ожидая, пока ее не вытащат на свет с помощью фокуса типа того, что мы применили к S(x) .
Это приводит к очевидному вопросу: а не обстоит ли дело подобным же образом и с дзета-функцией? Не случилось ли так, что бесконечная сумма, которую мы использовали для дзета-функции, — выражение (9.1) — описывает только часть этой функции? И у этой функции есть что-то еще, что нам только предстоит открыть? Может ли область определения дзета-функции
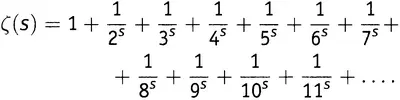
оказаться больше, чем просто «все числа, большие 1»?
Конечно может. Иначе зачем бы мы тут стали влезать во все эти подробности? Да, дзета-функция имеет значения при аргументах, меньших 1. На самом деле, как и функция 1/(1 − x ), она имеет значения при всех числах за единственным исключением x = 1.
Сейчас подходящий момент, чтобы привести график дзета-функции, который продемонстрировал бы все ее свойства в широком интервале значений. К сожалению, это невозможно. Как уже упоминалось, кроме как для простейших функций, обычно нет хорошего и надежного способа показать функцию во всем ее великолепии. Близкое знакомство с функцией требует времени, терпения и тщательного изучения. Можно, однако, изобразить дзета-функцию по кускам. На рисунках с 9.3 по 9.10 показаны значения ζ(s) для некоторых аргументов, находящихся слева от s = 1, хотя для этого потребовалось выбрать свой собственный масштаб на каждом графике. Понять, где мы находимся, можно, руководствуясь подписанными аргументами (на горизонтальной оси) и значениями (на вертикальной оси). При обозначении масштаба m указывает на миллион, tr на триллион, mtr обозначает миллион триллионов, a btr — миллиард триллионов.
Читать дальшеИнтервал:
Закладка:










