Джон Дербишир - Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.

Коротко говоря, когда s лишь немного меньше единицы (рисунок 9.3), значения функции очень большие по величине и отрицательные — как если бы при движении на запад при пересечении линии s = 1 значения внезапно переметнулись из бесконечности в минус бесконечность. Если продолжить путешествие по рисунку 9.3— т.е. устремлять s ближе и ближе к нулю, — то подъем вверх радикально замедляется. Когда s равно нулю, ζ(s) равна − 1/ 2. При s = −2 кривая пересекает ось s , т.е. ζ(s) равна нулю.

Рисунок 9.3.

Затем (мы по-прежнему двигаемся на запад, добравшись теперь до рисунка 9.4) график взбирается на относительно скромную высоту (в действительности до 0,009159890…), а после этого поворачивает вниз и снова пересекает ось при s = −4. График попадает в неглубокую впадину (−0,003986441…), а после нее снова взбирается вверх и пересекает ось при s = −6. Еще один невысокий пик (0,004194…), спуск до пересечения с осью при s = −8 и далее в несколько более глубокую впадину (−0,007850880…), затем пересечение с осью в точке −10, после чего уже довольно заметный пик (0,022730748…), пересечение с осью при s = −12, впадина поглубже (−0,093717308…), пересечение с осью при s = −14 и т.д.

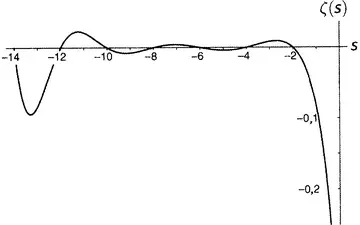
Рисунок 9.4.

Дзета-функция равна нулю при каждом отрицательном четном числе, а по мере продвижения на восток (рисунки от 9.5 до 9.10) последовательные пики и впадины быстро делаются все более и более значительными. Последняя показанная впадина расположена при s = −49.587622654 … , а глубина ее составляет около 305 507 128 402 512 980 000 000. Сами видите, как нелегко изобразить дзета-функцию на одном графике.

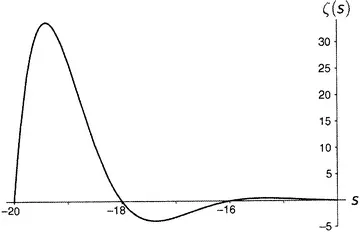
Рисунок 9.5.

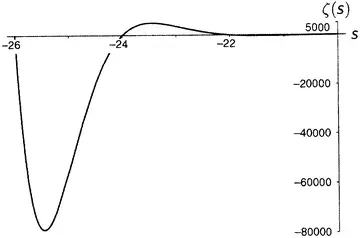
Рисунок 9.6.

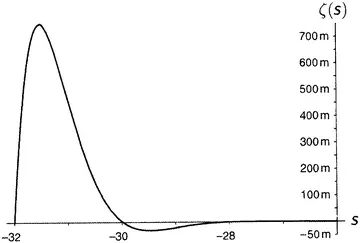
Рисунок 9.7.

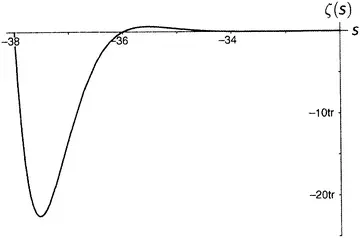
Рисунок 9.8.

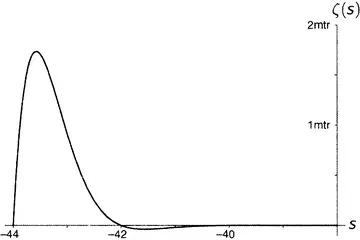
Рисунок 9.9.

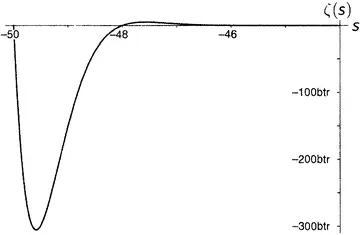
Рисунок 9.10.

Ho как я получил все эти значения ζ(s) для s , меньших 1? Мы уже видели, что бесконечный ряд из выражения (9.1)для этого непригоден. А что пригодно ? Если бы ради спасения своей жизни мне пришлось вычислить значение ζ (−7,5), как бы я к этому подступился?

Я не могу объяснить этого в полной мере, потому что такое объяснение требует слишком значительного погружения в математический анализ. Но я попробую передать общую идею. Сначала определим некоторую новую функцию, используя бесконечный ряд, слегка отличный от ряда в выражении (9.1). Это η- функция; η (читается «эта») — седьмая буква греческого алфавита. Определим η- функцию как

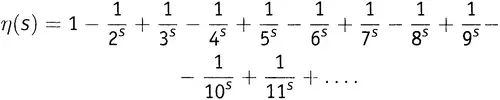
Грубая прикидка подсказывает, что у этой функции перспективы сходимости лучше, чем у выражения (9.1). Вместо непрестанного прибавления чисел здесь мы по очереди то прибавляем, то вычитаем, так что каждое следующее число до некоторой степени сокращает вклад предыдущего. Так оно и выходит. Математики в состоянии доказать — хотя здесь мы этим заниматься не будем, — что этот новый бесконечный ряд сходится всегда, когда s больше нуля. Это существенное улучшение по сравнению с выражением (9.1), которое сходится, только когда s больше единицы.

Но какая нам от всего этого польза в отношении дзета-функции? Для начала заметим, что в силу элементарных алгебраических правил A − B + C − D + E − F + G − H + … равно (A + B + C + D + E + F + G + H + …) минус 2× (B + D + F + H + …) . Поэтому функцию η(s) можно переписать как

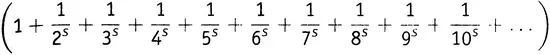
минус

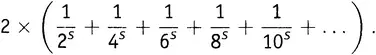
Первая скобка — это, конечно, ζ(s) . Вторую скобку легко упростить, пользуясь 7-м правилом действий со степенями: (ab) n = a nb n . Таким же образом каждое из этих четных чисел можно разбить в произведение вида 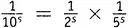, после чего можно вынести 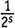в качестве множителя перед всей скобкой. А что останется в скобке? Там останется ζ(s) ! Коротко говоря,

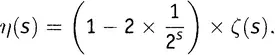
или, переписав это «наоборот» и слегка причесав, получаем

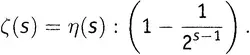
Вот. Это означает, что если нам удастся узнать какое-то значение η(s) , то мы немедленно будем знать и значение ζ(s) . А поскольку можно узнать значения η(s) между 0 и 1, можно получить и значение ζ(s) в этом промежутке, несмотря на то что «официальный» ряд для ζ(s) там не сходится.

Пусть, например, s равно 1/ 2. Если сложить 100 членов ряда для η ( 1/ 2), то получится 0,555023639…; если сложить 10 000 членов, получится 0,599898768…. В действительности значение η ( 1/ 2) составляет 0,604898643421630370…. (Существуют определенные приемы позволяющие вычислять такое без необходимости сложения мириад членов.) Вооруженные всем этим, мы можем вычислить значение ζ ( 1/ 2) оно оказывается равным −1,460354508…, что выглядит очень правдоподобно, если судить по первому графику из приведенного выше набора.

Но задержимся на мгновение. Не устроили ли мы тут игру в наперстки с двумя бесконечными рядами, один из которых сходится при аргументе s = 1/ 2, а другой — нет? Ну, строго говоря, мы действуем не совсем по правилам, и я обошелся довольно безответственно с той математикой, на которой здесь все основано. Однако же я получил правильный ответ, причем этот фокус можно повторить для любого числа между нулем и единицей (не включая ее) и получить правильное значение для ζ(s) .

За исключением одного только s = 1, где ζ(s) не имеет значения, мы можем теперь предъявить значение дзета-функции для любого числа s , большего нуля. А как насчет аргументов равных нулю или меньших нуля? Вот здесь все по-настоящему круто. Один из результатов в работе Римана 1859 года состоит в доказательстве формулы, впервые предложенной Эйлером в 1749 году, которая выражает ζ( 1 − s) через ζ(s) . Таким образом, если мы желаем узнать, например, значение ζ (−15), то надо просто вычислить значение ζ (16) и подставить его в эту формулу. Это, правда, неслабая формула, и я привожу ее главным образом для полноты картин: [75]