Джон Дербишир - Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.

Чтобы получить сбалансированное представление о комплексных числах, неплохо бы понять, как вообще современные математики воспринимают числа. Это мы сейчас и рассмотрим, включив в наш рассказ заодно и комплексные числа. Не нервничайте пока слишком сильно по поводу того, что же они собой представляют: подробности последуют очень скоро, а в несколько следующих абзацев комплексные числа включены просто для полноты.

Итак, как же современный математик воспринимает числа? В виде ажурных букв, вот как! В виде букв N, Z, Q, Rи C. {1} Я пытался придумать какое-нибудь идиотское, а потому застревающее в памяти мнемоническое правило для их запоминания, но не смог изобрести ничего, кроме Nine Zulu Queens Ruled China. [92]

А может, я и поспешил немного. Вот альтернативный ответ на тот же вопрос: математики воспринимают числа как набор сидящих одна в другой матрешек. Вот таких.

• Самая внутренняя матрешка: натуральные числа 1, 2, 3, 4, 5, ….

• Следующая матрешка: все целые числа. Другими словами, натуральные числа вместе с нулем и отрицательными целыми (такими как −12).

• Следующая матрешка: рациональные числа. Другими словами, все целые вместе с положительными и отрицательными дробями (например, числа 3/ 2, − 1/ 917 635, 1000 000 000 001/ 6).

• Следующая матрешка: вещественные числа. Другими словами, рациональные вместе с иррациональными, такими как √2, π, e . (Из примечания [18]в главе 3.vi мы помним, что древние греки открыли существование чисел, которые не являются ни целыми, ни дробями, — иррациональных чисел.)

• Внешняя матрешка: комплексные числа .

Уместно сделать несколько замечаний по поводу такой организации. Во-первых, числа из каждой матрешки записываются характерным для каждой из них способом.

• Натуральные числа обычно записываются так: 257.

• Целые могут иметь перед собой знак, например −34.

• Рациональные числа чаще всего записываются в виде дробей. В том, что касается записи в виде дроби, рациональные числа бывают двух видов. Те, величина которых (без учета знака) меньше единицы, называются «правильными дробями», а все остальные — «неправильными». Правильная дробь записывается таким образом: 14/ 37. Неправильную дробь можно записать двумя способами: как собственно неправильную дробь 13/ 9или же в «смешанном» виде (с выделенной целой частью) 1 4/ 9.

• Наиболее важным вещественным числам присвоены специальные обозначения, такие как π и e . Многие другие можно выразить «в замкнутом виде», подобно 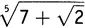или π 2/6. Когда больше ничего нельзя сделать или же просто для того чтобы оценить реальное численное значение вещественного числа, его записывают в виде десятичной дроби, как правило, с многоточием в конце, которое означает: «Это не все! если надо, можно добавить сюда еще десятичные разряды», например −549,5393169816448223…. Их можно округлять, скажем, до «пяти знаков после запятой» −549,53932, или до «пяти значащих цифр» −549,54, или с любой другой точностью.

• Комплексные числа выглядят так: −13,052 + 2,477 i . О них мы еще поговорим.

Следующее, что нужно заметить, — это что обитатели каждой матрешки являются привилегированными гражданами следующей (внешней) и при желании могут быть записаны в стиле, принятом для этой внешней матрешки:

• Натуральные числа (скажем, 257) — это привилегированные целые числа, и их можно записать, поставив перед ними знак плюс, как +257. При виде целого числа со знаком плюс перед ним мы думаем: «Натуральное!»

• Целые (скажем, −27) — это привилегированные рациональные числа, и их можно записать в виде дроби, знаменатель которой равен 1, как − 27/ 1. При виде рационального числа со знаменателем 1 мы думаем: «Целое!»

• Рациональные числа (скажем, 1/ 3) — это привилегированные вещественные числа, и их можно записать в виде десятичных дробей, как 0,33333333…. Насчет рациональных чисел интересен тот факт, что при записи рационального числа в виде десятичной дроби знаки после запятой рано или поздно обязательно начнут повторяться (если только они вообще не исчерпаются, как, скажем, в числе 7/ 8= 0,875). Рациональное число 65 463/ 27 100, например, в виде десятичной дроби выглядит следующим образом:

Все рациональные числа демонстрируют такие повторы, но ни одно из иррациональных ничего подобного не делает. Другими словами, иррациональное число не может проявлять никакого порядка в последовательности своих знаков после запятой. Число

ясно демонстрирует некий порядок, и несложно заранее сказать, каков в нем сотый знак после запятой, или миллионный, или триллионный. (Спорим? Это соответственно 5, 1 и 1). Однако число это иррациональное. Когда же мы видим вещественное число, в котором знаки после запятой повторяются, мы думаем: «Рациональное!»

• Любое вещественное число можно записать как комплексное. Например, √2 записывается в виде комплексного числа как √2 + 0 i . Подробности ниже.

(В этом списке можно и перескочить через несколько ступенек и записать, скажем, натуральное число как вещественное: 257,000000000….)

Каждое семейство чисел — каждая из матрешек — обозначается ажурной буквой: N— семейство всех натуральных чисел, Z— целых, Q— рациональных, a R— вещественных. Каждое семейство в определенном смысле содержится внутри следующего. И каждое расширяет возможности математики, позволяя делать что-то такое, чего нельзя было делать с предыдущей матрешкой. Например, Zпозволяет получить ответ для вычитания любого целого числа из любого целого, чего не удавалось сделать, оставаясь в N(7 − 12 =?). Подобным же образом Qпозволяет получить ответ для деления на любое число (кроме нуля), чего не удавалось сделать, оставаясь в Z((−7):(−12) =?). И наконец, Rоткрывает дорогу анализу — математике пределов, — поскольку любая сходящаяся бесконечная последовательность чисел в Rимеет предел (что неверно для Q).

(Вспомним последовательности и ряды, с которыми мы встретились в конце главы 1. Все они состояли из рациональных чисел. Некоторые из них сходились к 2, или 2/ 3, или 1 1/ 2— т.е. их пределы также оказывались рациональными. Но другие, напротив, сходились к √2, или π , или e — иррациональным числам. Таким образом, бесконечная последовательность чисел из Qможет сходиться к пределу, который не лежит в Q. Математический профессиональный термин: Qне является полным. Напротив, Rполно, как полно и С. Эта идея пополнения Qприобретет новое значение, когда в главе 20.v мы будем говорить о p- адических числах.)