Джон Дербишир - Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.

Ο большое — это способ наложить ограничение на величину функции, когда аргумент устремляется к (как правило) бесконечности.

Функция A есть Ο большое от функции B, если для достаточно больших аргументов величина A никогда не превосходит некоторого фиксированного кратного величины B .

Вслед за Паулем Тураном рассмотрим Ο большое от единицы. «Единица» здесь понимается как функция, причем функция простейшего вида. Ее график — горизонтальная прямая, проходящая на высоте 1 над горизонтальной осью. Для вообще любых аргументов значение этой функции равно… просто 1. Ну и что же тогда означает, что функция f(x) есть Ο большое от единицы? По только что данному определению это означает, что, когда аргумент x уходит на бесконечность, f(x) никогда не превзойдет некоторого фиксированного кратного 1 — другими словами, график функции f(x) навсегда останется ниже некоторой горизонтальной прямой. Это полезная информация о данной нам функции f(x) . Существует множество функций, для которых это не так. Это не так, например, для x 2и для x в любой положительной степени, ни для e x ни даже для ln x .

На самом деле Ο большое означает еще кое-что, кроме этого. Заметим, что в определении сказано «величина A». Это означает «значение A без учета знака». Величина числа 100 есть 100; величина числа −100 есть также 100. Ο большое не принимает в расчет знак минус. Сказать, что некоторая функция f(x) есть Ο большое от единицы, означает сказать, что f(x) навсегда заключена между двумя горизонтальными прямыми, одна из которых проходит выше горизонтальной оси, а другая проходит на таком же расстоянии ниже.

Как уже говорилось, очень многие функции не являются Ο большим от единицы. Простейшая из них — это функция x , то есть функция, значения которой всегда равны ее аргументу. Ее график — диагональная прямая, покидающая рисунок в верхнем правом углу. Ясно, что она не заключена между какими бы то ни было горизонтальными прямыми. Вне зависимости оттого, сколь широко вы расположите эти горизонтальные прямые, функциях рано или поздно вырвется за их пределы. Это останется верным, если уменьшить наклон. Функции 0,1 x (показана на рисунке 15.1), 0,01 x , 0,001 x и 0,0001 x все в конце концов прорвутся через любые горизонтальные прямые, которые вы установите в качестве ограничения. Ни одна из них не является Ο большим от единицы.

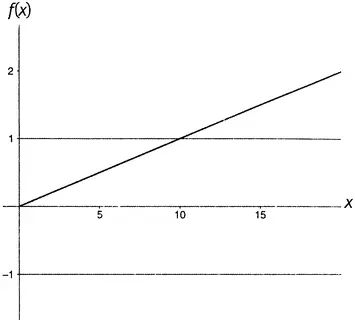
Рисунок 15.1.Функция 0,1 x не есть Ο большое от единицы.

Этим иллюстрируется и еще один аспект Ο большого. Ο большое игнорирует не только знаки, но и множители. Если A есть Ο большое от B , то таковыми же будут 10 A , 100 A и 1000 000 A ; таковыми будут и одна десятая A одна сотая A одна миллионная A. Ο большое не сообщает нам о точном темпе роста — для этого у нас есть производные. Она сообщает о типе роста. Функция «единица» вообще не имеет никакого темпа роста — она намертво постоянная. Функция, являющаяся Ο большим от единицы, никогда не возрастет быстрее этого. Она может выделывать всякое другое: прижиматься к нулю, колебаться без конца внутри ограничивающих ее прямых или же подходить к одной из ограничительных линий все ближе и ближе, но она никогда не взовьется внезапно вверх и не нырнет внезапно вниз, прорываясь через эти линии и оставаясь после этого снаружи.

Приведенные функции 0,1 x , 0,01 x , 0,001 x и 0,0001 x — не Ο большое от единицы; все они — Ο большое от x . Такова же и любая другая функция, которая остается навсегда заключенной в «куске пиццы» между прямой ax и ее зеркальным отражением −ax. На рисунке 15.2 приведен пример функции, которая не остается в таких пределах. Это 0,1 x 2— квадратичная функция. Не важно, сколь широким вы сделаете этот кусок пиццы — т.е. не важно, сколь велико значение a , — график функции 0,1 x 2рано или поздно прорвется через верхнюю границу.

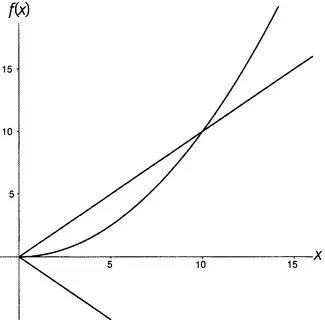
Рисунок 15.2.Функция 0,1 x 2не есть Ο(х).

Теперь мы можем оценить значение результата фон Коха 1901 года. Если Гипотеза Римана верна, то при x , стремящемся к бесконечности, абсолютная разность между π(x) и Li (x) — т.е. или Li (x) − π(x) , или π(x) − Li (x) , что не важно, потому что Ο большому нет дела до знаков, — остается заключенной между двумя ограничивающими кривыми. Ограничивающие кривые — это C√x ∙ln x и ее зеркальное отражение, где C — некоторое число. Остаточный член может делать что хочет между этими двумя кривыми, но он никогда не выберется наружу и никогда не вырвется внезапно из-под их контроля. Разность между π(x) и Li(x) есть Ο большое от √x ∙ln x .

На рисунке 15.3приведен пример функции, которая есть Ο ( √x ∙ln x ). Там показаны: 1) кривая √x ∙ln x (верхняя половина отдаленно напоминающей параболу кривой), 2) зеркально отраженная кривая −√x ∙ln x (нижняя половина) и 3) придуманная для иллюстрации и ничего особенно не выражающая функция, которая есть Ο ( √x ∙ln x ). Буква m обозначает миллион, ведь вещи подобного рода интересны только для больших аргументов. Стоит отметить, что "функция Дербишира" в действительности на некоторое время вырывается за пределы ограничивающих ее кривых при аргументах, равных примерно 200 миллионам. Это не страшно, поскольку больше она никогда такого не делает. Начиная с некоторой точки — и навсегда после нее — функция остается в пределах границ. Верьте мне, что она там остается, хотя по понятным причинам я и не могу показать вам всю функцию до бесконечности. Ο большое принимает во внимание исключения из правил при малых аргументах (а такие исключения — общее место в теории чисел, взять хотя бы утверждение «все простые числа нечетные… кроме самого первого»).

Рисунок 15.3.Функция Дербишира есть Ο (√ x ∙ln x ).

Можно заметить еще, что, поскольку Ο большое не принимает во внимание множители, масштаб по вертикали совершенно произволен. Важны лишь конфигурация — форма ограничивающих кривых — и тот факт, что начиная с какого-то места наша функция навсегда заключена между ними.

Результат фон Коха 1901 года [135]— а именно утверждение, что, если Гипотеза Римана верна, то π(x) = Li (x) + Ο (√ x ∙ln x ), — один из первых примеров определенного типа результатов, которыми сейчас полна теория чисел, — результатов, которые начинаются словами «Если Гипотеза Римана верна, то…». Если окажется, что Гипотеза Римана не верна, то немалую часть теории чисел придется переписывать.