Джон Дербишир - Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.

Как только вы смогли это увидеть, перемножение бесконечного числа скобок больше не проблема. В ответе будет сумма — разумеется, бесконечная — членов, каждый из которых получен путем выбора одного числа из каждой скобки и перемножения всего, что выбрали. Если сложить результаты всех таких возможных выборов, то и получится ответ. Однако в том виде, как эта процедура описана, она все еще выглядит несколько устрашающей. Согласно сказанному, каждый член в нашей бесконечной сумме есть бесконечное произведение. Да, так оно и есть, но, поскольку каждая скобка в правой части выражения (15.1)содержит 1, наша жизнь делается приятнее за счет того, что мы будем выбирать бесконечное число единиц и лишь конечное число не-единиц. В конце концов, поскольку каждый не-единичный член в каждой скобке есть число между − 1/ 2и 0, перемножение бесконечно большого числа таких членов дает результат, величина которого (я имею в виду — без учета знака) заведомо не больше, чем ( 1/ 2) ∞, а это равно нулю! Теперь смотрите, как я построю бесконечную сумму.

Первый член в бесконечной сумме: берем 1 из каждой скобки. Это даст бесконечное произведение 1×1×1×1×1×…, значение которого есть, конечно, просто 1.

Второй член: берем 1 из всех скобок, кроме первой. Из первой же возьмем 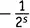. Это даст бесконечное произведение 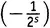×1×1×1×1×…, которое равно просто .

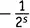Третий член: берем 1 из каждой скобки, кроме второй. А из второй возьмем 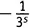. Это даст бесконечное произведение 1× 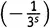×1×1×1×…, что равно просто .

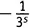Четвертый член… Я думаю, понятно, что, если брать 1 из каждой скобки, кроме n -й, мы получим слагаемое равное 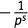, где p — n -е простое число. Итак, получилась бесконечная сумма вида (15.3):

Но это еще не конец. При перемножении скобок возникает сумма всех возможных членов, получаемых взятием одного числа из каждой скобки. Предположим, мы выбрали 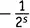из первой скобки, 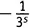из второй и 1 из всех остальных. Это дает 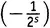× ×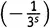1×1×1×…, что равно 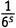. Похожие вещи мы получим из каждой возможной пары выборов не-единиц. Выбирая из третьей скобк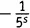и и 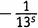из шестой, а единицы из всех остальных, получаем член, равный .

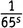(Заметим, что здесь работают два простых правила арифметики. Одно — это правило знаков, гласящее, что минус умножить на минус дает плюс, а другое — 7-е правило действий со степенями, согласно которому (x×y) n= x n×y n .)

Так что наряду с членами, уже собранными в выражении (15.3), имеется новый набор, каждый член в котором происходит из каждой пары простых чисел, как 5 и 13, и которые все входят со знаком плюс. Таким образом, выражение (15.3)разрослось до такого:

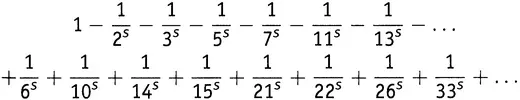
где каждое число во второй строке есть произведение двух различных простых.

А ведь мы едва начали нашу деятельность по перемножению бесконечного числа скобок. Следующий шаг состоит в том, чтобы перебрать все возможные способы выбрать три не-единицы (при всех остальных единицах). Например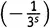, 1× ×1×1× 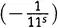× ×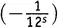1×1×…, из чего возникает 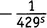.Теперь результат разрастается до

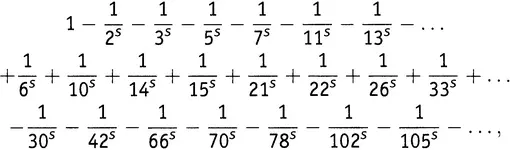
где каждое число в третьей строке есть произведение трех различных простых.

В предположении, что мы продолжаем так поступать, а также в предположении, что получающиеся члены можно переставлять, как мы пожелаем, выражение (15.1)превращается в следующее (15.4):

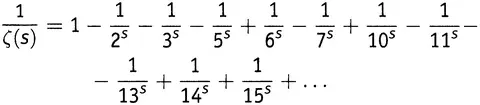
Натуральные числа в правой части — это… что? Это заведомо не все натуральные числа: 4, 8, 9 и 12 там отсутствуют. Но и не простые: присутствующие там 6, 10, 14 и 15 не являются простыми. Если оглянуться на процесс перемножения этого бесконечного количества скобок, то станет ясно, что ответ такой: каждое натуральное число, которое равно произведению нечетного числа (включая 1) различных простых, взятое со знаком минус, и, кроме того, каждое натуральное число, которое равно произведению четного числа различных простых, взятое со знаком плюс. Отсутствуют такие числа, как 4, 8, 9, 12, 16, 18, 20, 24, 25, 27, 28, … — т.е. числа, которые делятся на квадрат некоторого простого.

Поприветствуем функцию Мебиуса! Она названа по имени немецкого математика и астронома Августа Фердинанда Мебиуса (1790–1868). [137]

Рисунок 15.4.Лента Мебиуса и муравей на ней.

В наше время ее общепринято обозначать греческой буквой μ , что произносится как «мю» — греческий эквивалент буквы «м». [138]Приведем полное определение функции Мебиуса.

• Ее область определения есть N , то есть все натуральные числа 1, 2, 3, 4, 5, ….

• μ (1) = 1.

• μ ( n ) = 0, если среди делителей числа n есть квадрат.

• μ ( n ) = −1, если число n простое или является произведением нечетного числа различных простых чисел.

• μ ( n ) = 1, если число n является произведением четного числа различных простых чисел.

Такое определение функции может показаться вам страшно громоздким. Однако функция Мебиуса приносит колоссальную пользу в теории чисел и далее в этой книге будет играть ведущую роль. В качестве примера приносимой ею пользы заметим, что все трудоемкие алгебраические действия, через которые нам пришлось продираться, сводятся к изящному выражению (15.5):

B истории Гипотезы Римана наряду с самой функцией μ(n) не меньшую роль играет ее нарастающее значение, т.е. результат сложения μ (1) + μ (2) + μ (3) + … + μ ( k ) для некоторого числа k . Так определяется «функция Мертенса» М(k) . Ее первые 10 значений (т.е. значения при k = 1, 2, 3, …, 10) равны 1, 0, −1, −1, −2, −1, −2, −2, −2, −1. Функция M(k) весьма нерегулярна — она совершает колебания в обе стороны вокруг нулевого значения в стиле, который математики называют «случайными блужданиями». Для аргументов, равных 1000, 2000, …, 10 000, ее значения равны 2, 5, −6, −9, 2, 0, −25, −1, 1, −23. Для аргументов миллион, 2 миллиона, …, 10 миллионов ее значения равны 212, −247, 107, 192, −709, 257, −184, −189, −340, 1037. Если не обращать внимания на знаки, то видно, что величина функции M(k) возрастает, но помимо этого никакой ясной картины не просматривается.