Джон Дербишир - Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике.

А есть ли какой-нибудь результат типа Ο большого для остаточного члена Li (x) − π(x) , который не зависел бы от справедливости Гипотезы Римана? О да. Среди специалистов по аналитической теории чисел долгие годы любимым спортом был поиск все лучших и лучших формул типа Ο большого для остаточного члена. Но ни один не может сравниться с Ο (√ x ∙ln x ). Это абсолютно лучшее, наиболее точное ограничение на остаточный член, известное к настоящему моменту. Правда, раз оно зависит от справедливости Гипотезы, мы не можем быть полностью уверены, что оно верно. Все те оценки остаточного члена, в справедливости которых мы уверены, менее точны, чем эта. Соответствующая параболическая кривая на рисунке 15.3несколько шире, причем различие делается все более заметным по мере того, как x уходит на бесконечность. Если же Гипотеза Римана верна, то среди всех известных оценок остаточного члена выражение Ο (√ x ∙ln x ) является наилучшим возможным — наиболее точной формулой типа Ο большого. Оно же и простейшее. При этом все формулы, которые были доказаны без предположения о справедливости Гипотезы, выглядят достаточно уродливо. Вот наилучшая из тех, что известны мне на данный момент:

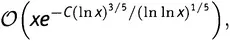
где С — некоторое постоянное число. Ни одна из других подобных формул на вид не проще этой.

Сравним результат фон Коха 1901 года с выделенными курсивом словами в восьмой проблеме Гильберта, приведенной в главе 12.ii. Гильберт перекликался с Риманом, написавшим в своей работе 1859 года, что приближение функции π(x) функцией Li (x) «верно только по порядку величины x 1/2». Ну а √x есть, конечно, попросту x 1/2. Более того, в главе 5.iv мы видели, что ln x растет медленнее, чем любая положительная степень x , даже самая ничтожно малая. Это можно выразить в терминах Ο большого таким образом: для любого сколь угодно малого числа ε выполнено ln x = Ο(x ε) . А следовательно (это, правда, не сразу очевидно, но в действительности несложно доказать), можно подставить x ε вместо ln x в выражение Ο ( √x ∙ln x ); а поскольку √x — это просто x 1/2, можно сложить степени и получить Ο ( x 1/2+ ε ). Таким путем получается довольно распространенный вид результата фон Коха: π(x) = Li (x) + Ο ( x 1/2+ ε ). Символ ε настолько часто используется для исчезающе малых чисел, что слова «… для любого сколь угодно малого ε » здесь подразумеваются.

Заметим, однако, что, делая эту подстановку, мы слегка ослабили результат фон Коха. Из того, что «остаточный член есть Ο ( √x ∙ln x )», следует, что «остаточный член есть Ο ( x 1/2+ ε )», но обратное неверно. Эти два утверждения не являются точно эквивалентными. Такое происходит, потому что, как мы видели в главе 5.iv, не только ln x растет медленнее, чем любая степень x , но (ln x ) N обладает тем же свойством при любом положительном N . Так что если бы результат фон Коха утверждал, что остаточный член есть Ο ( √x ∙(ln x ) 100), то мы все равно в качестве альтернативного вида вывели бы Ο ( x 1/2+ ε )!

Однако запись результата фон Коха в этом слегка ослабленном виде Ο ( x 1/2+ ε ) хороша тем, что наводит на размышления. Риман был почти прав в том же смысле, в каком логарифмическая функция есть почти x 0; порядок величины есть не х 1/2, а x 1/2+ ε . Если учесть, какие средства имелись у него в наличии, каким было общее состояние знания в данной области и какие численные данные были доступны в то время, то риманово x 1/2все равно должно считаться прозрением потрясающей глубины. [136]

Вводя Ο большое, я начал с истории, так что сейчас, прощаясь с ним, расскажу еще одну. Суть ее в том, что математики, как и другие специалисты, иногда любят напустить туману, чтобы отпугнуть и смутить профанов.

На конференции в Курантовском институте летом 2002 года (см. главу 22) я разговаривал по поводу своей книги с Питером Сарнаком. Питер — профессор математики в Принстонском университете и специалист по теории чисел. Я упомянул, что пытаюсь придумать, как объяснить Ο большое тем читателям, кто с ним незнаком. «О, — сказал Питер, — вам надо бы поговорить с моим коллегой Ником (т.е. Николасом Кацем — он тоже профессор в Принстоне, но занимается в основном алгебраической геометрией). Ник ненавидит Ο большое. Никогда его не использует». Я это проглотил, но взял на заметку, рассчитывая, что смогу придумать, как это использовать в книге. В тот же вечер мне случилось разговаривать с Эндрю Уайлсом, который очень хорошо знает и Сарнака, и Каца. Я упомянул нелюбовь Каца к Ο большому. «Чепуха, — сказал Уайлс, — они просто над вами потешаются. Да Ник все время его использует». И будьте уверены, Кац использовал его в лекции на следующий же день. Своеобразное чувство юмора у математиков.

Оставим Ο большое. Теперь перед нами функция Мебиуса. Есть несколько способов ввести функцию Мебиуса. Подойдем к ней со стороны Золотого Ключа.

Возьмем Золотой Ключ и перевернем его вверх ногами, т.е. возьмем обратную величину к каждой стороне равенства в выражении (7.2). Очевидно, если A = B и при этом ни A, ни B не равны нулю, то 1 /A = 1 /B. Получаем (15.1)

Теперь раскроем скобки в правой части. На первый взгляд, это сильно сказано: как-никак, сомножителей в скобках бесконечно много. На самом деле процедура требует несколько большего внимания и обоснования, чем мы можем здесь ей уделить, но в конце концов мы получим полезный и верный результат, так что в данном случае цель оправдывает средства.

Раскрытие скобок все мы изучали в курсе элементарной алгебры. Чтобы перемножить (а + b)(p + q) , сначала умножаем a на (p + q), что дает ар + aq. Затем умножаем b на (p + q), что дает bp + bq. А потом, поскольку в скобках у нас a плюс b , мы складываем вместе то, что получилось, и окончательный ответ имеет вид ap + aq + bp + bq . Если надо перемножить три скобки (а + b)(p + q)(u + v), то повторение этих действий дает apu + aqu + bpu + bqu + apv + aqv + bpv + bqv. Перемножение четырех скобок (а + b)(p + q)(u + v)(x + у) дает

Грандиозность того, что получается, начинает внушать некоторые опасения. А ведь нам предстоит перемножить бесконечное число скобок! Фокус состоит в том, чтобы посмотреть на это дело глазами математика. Из чего составлено выражение (15.2)? Ну, это сумма некоторого числа членов. Как эти члены выглядят? Выберем наугад какой-нибудь один из них, скажем aqvy . Сюда входит a из первой скобки, q из второй, v из третьей и y из четвертой. Это произведение, составленное из чисел, выбранных по одному из каждой скобки. И все выражение целиком получается в результате всех возможных комбинаций того, как мы выбираем эти числа из скобок.