Генри Дьюдени - Пятьсот двадцать головоломок
- Название:Пятьсот двадцать головоломок
- Автор:
- Жанр:
- Издательство:Мир
- Год:1975
- Город:Москва
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Генри Дьюдени - Пятьсот двадцать головоломок краткое содержание
Генри Э. Дьюдени по праву считается классиком занимательной математики. Многие его задачи, породив обширную литературу и вызвав многочисленные подражания, вошли в ее золотой фонд.
В предлагаемой книге собрано 520 задач и головоломок Дьюдени по арифметике, алгебре, геометрии, разрезанию и составлению фигур. Читателя ждет встреча с постоянно действующими героями Дьюдени — семейством Крэкхэмов, профессором Рэкбрейном и др.
Книга доставит удовольствие всем любителям занимательной математики.
Пятьсот двадцать головоломок - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
34
Можно сказать иначе: вероятность того, что наугад взятое число делится на 11, равна . — Прим. перев.
35
См. примечание на стр. 38.
36
Здесь [ a ] означает целую часть числа a , то есть наибольшее целое число, не превосходящее a . См. также примечание на стр. 38. — Прим. перев.
37
Целой частью числа называется наибольшее целое число, не превосходящее данное. — Прим. перев.
38
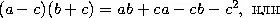
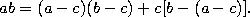
Выбрав a = 879, b = 993 и c = 7, мы и получим правило, по которому действует автор. — Прим. перев.
39
Строго говоря, это еще не доказательство, но его можно легко получить, пользуясь свойствами эллипса. Булавки должны располагаться в фокусах эллипса A к B . CD представляет собой большую, a EF — малую оси эллипса; обозначим их соответственно через 2 a и 2 b , а фокусное расстояние AB через 2 c . Тогда из треугольника AGF получим AF = 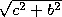 . Но в силу свойств эллипса
. Но в силу свойств эллипса 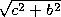 = a , то есть AF = CD , что и требовалось. — Прим. перев.
= a , то есть AF = CD , что и требовалось. — Прим. перев.
40
Эта кривая называется линией погони. — Прим. перев.
41
См. решение задачи 403. — Прим. перев.
42
Можно сказать, что Дьюдени доказал локальную, а не глобальную теорему. — Прим. перев.
43
Из n предметов m можно выбрать C n m = 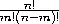 способами. Общая сумма способов равна 1 + C n 1+ C n 2+ ... + C n n = (1 + 1) n = 2 n . Сюда вошел и «способ», при котором мы вообще ничего не выбираем (не дарим ни одной картины). Исключив его, мы и получим 2 n - 1. — Прим. перев.
способами. Общая сумма способов равна 1 + C n 1+ C n 2+ ... + C n n = (1 + 1) n = 2 n . Сюда вошел и «способ», при котором мы вообще ничего не выбираем (не дарим ни одной картины). Исключив его, мы и получим 2 n - 1. — Прим. перев.
44
Five ( англ. ) — пять.
45
Имеются в виду шансы сесть на поезд. — Прим. перев.
Интервал:
Закладка:






![О Генри - Через двадцать лет [After Twenty Years]](/books/1083375/o-genri-cherez-dvadcat-let-after-twenty-years.webp)

