Генри Дьюдени - Кентерберийские головоломки

У торговца чаем было пять банок кубической формы, которые стояли в ряд на прилавке, как вы видите на рисунке. Каждая коробка на каждой из шести сторон имела рисунок, так что всего было 30 рисунков. Но один из рисунков первой коробки повторялся на четвертой, адва других рисунка четвертой коробки повторялись на третьей. Следовательно, имелось лишь 27 различных рисунков. Владелец всегда держал первую коробку в одном конце ряда и никогда не ставил бок о бок третью и пятую коробки.

Один покупатель, узнав об этом, подумал, что будет хорошей головоломкой выяснить, сколькими способами коробки можно разместить на прилавке так, чтобы при этом порядок пяти рисунков на лицевой стороне не повторялся. Оказалось, что это довольно крепкий орешек. Сумеете ли вы найти ответ, не запутавшись окончательно? Разумеется, два одинаковых рисунка могут оказаться одновременно на лицевой стороне, ибо весь вопрос заключается в их порядке.

92. Четыре поросенка.Каждого из четырех поросят помещают в отдельный свинарник таким образом, что хотя каждый из 36 свинарников расположен на одной прямой (горизонтальной, вертикальной или диагональной) по крайней мере с одним поросенком, все же ни один поросенок не находится на одной прямой с другим.

Сколько существует различных способов распределить поросят по свинарникам при этих условиях? Повернув рисунок, вы получите еще три расположения, а сделав это перед зеркалом, получите еще четыре. Эти расположения мы не считаем различными.

93. Перенумерованные кубики.Дети, которых вы видите на рисунке, нашли, что с помощью перенумерованных кубиков можно придумать много поучительных и интересных головоломок. Имеется десять кубиков, на каждом из которых нанесена одна цифра – 1, 2, 3, 4, 5, 6, 7, 8, 9 или 0. В данный момент дети заняты головоломкой, в которой требуется разделить кубики на две группы, по пять кубиков в каждой, а затем расположить их так, что если в каждую из групп поставить в надлежащем месте знак умножения, то получатся произведения, одинаковые в каждой группе.

Число возможных решений весьма значительно, но дети нашли такое решение, при котором произведение оказалось наименьшим из возможных. Так, если 3485 умножить на 2, то получится 6970, и это же произведение получится при умножении 6970 на 1. Вы обнаружите, что вполне посильно найти любой меньший результат.

Моя головоломка состоит в том, чтобы отыскать результат, наибольший из возможных. Разбейте кубики на любые две группы, по пять кубиков в каждой, и поставьте в нужных местах знак умножения, чтобы при этом одинаковое произведение в каждой группе оказалось максимальным. Вот и все, но этот орешек не так-то легко раскусить. Разумеется, не разрешается использовать дроби или применять какие-либо иные трюки. Головоломка в той достаточно простой форме, в которой я ее предлагаю, довольно интересна. Быть может, следует добавить, что множители могут быть двузначными.

94. Лисы и гуси.Вот небольшая головоломка с фишками, которую читатель, наверное, найдет занимательной. Сделайте диаграмму любого удобного размера, подобную той, что показана на рисунке, и возьмите шесть фишек: три из них изображают лис, а три другие – гусей. Поставьте гусей на кружки 1, 2 и 3, а лис – на кружки 10, 11 и 12.

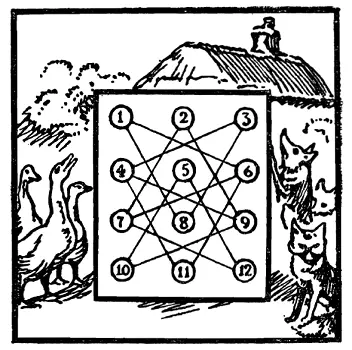
Головоломка состоит в следующем. Передвигая поочередно по одной фишке (то лис, то гусей) вдоль прямой от одного кружка к следующему, попытайтесь провести лис на кружки 1, 2 и 3, а гусей – на кружки 10, 11 и 12 (то есть поменяйте их местами) за наименьшее возможное число ходов.

Но при этом вы должны быть внимательны и не позволять лисам и гусям находиться в пределах досягаемости друг друга, иначе могут возникнуть неприятности. Это правило, как легко понять, запрещает на первом ходу передвинуть лису из 11 на 4 или 6, ибо тогда она оказалась бы в пределах досягаемости гуся. Оно также запрещает передвинуть лису с 10 на 9 или с 12 на 7. Если вы пойдете с 10 на 5, то следующий ход гусем может быть с 2 на 9, чего нельзя было бы делать, если бы предварительно лиса не ушла с 10. Наверное, очевидно, что на кружке одновременно может находиться лишь одна лиса или один гусь. Чему равно наименьшее число ходов, необходимое для того, чтобы поменять местами лис и гусей?

95. Стол Робинзона Крузо.Вот любопытное извлечение из дневника Робинзона Крузо. Его нельзя найти в новых изданиях. А жаль…

«На третий день утром, когда ветер за ночь ослабел, я вышел на берег, надеясь найти пишущую машинку и другие полезные вещи, выброшенные с разбитого корабля; но все, что мне попалось на глаза, – это доска со множеством дырок. Мой человек Пятница много раз говорил, что нам совершенно необходим квадратный стол для чаепитий, и я задумался, как использовать с этой целью данную доску. А поскольку то долгое время, что Пятница проводил со мной, я еще не использовал для того, чтобы вложить в его голову основы полезных знаний, то он был немало удивлен, когда я сказал, что хочу сделать из найденной доски стол, на крышке которого не будет ни одной дырки.

Пятница печально размышлял, как это можно сделать, и пришел в совершенное уныние, когда я сказал, что крышка должна состоять не более, чем из двух кусков, соединенных вместе. Однако я научил его, как это можно сделать, чтобы стол был возможно большим. Если быть честным, меня позабавили его слова:

– Мой народ поступает много лучше: у нас просто затыкают дырки, чтобы в них не проваливался сахар».

На рисунке приведены точные пропорции доски с расположением на ней пятнадцати дырок. Как Робинзон Крузо сделал из нее наибольшую возможную квадратную крышку стола, состоящую из двух кусков и не содержащую дырок?

96. Пятнадцать фруктовых садов.В графстве Девоншир, славящемся своим сидром, пятнадцать жителей одной деревни были одержимы прекрасным духом дружеского соперничества на почве разведения яблоневых садов. И несколько лет назад они захотели экспериментально разрешить некоторое расхождение во мнениях относительно того, как следует выращивать яблони. Одни считали, что яблоням требуется много света и воздуха, тогда как другие твердо стояли на том, что их следует сажать достаточно тесно, дабы они получали тень и защиту от холодных ветров. Решено было посадить несколько саженцев, разное число в каждом саду, и сравнить результаты.