Яков Перельман - Математика для любознательных

- Много ли времени потребует вся работа вашей машины?

- Времени, конечно, порядочно. Но простота конструкции моей машины дает возможность значительно сократить необходимое время. Ведь работа машины сводится ко вращению небольших шестерен, а скорость вращения можно технически довести до весьма высокой степени. Турбина Лаваля делает 30.000 оборотов в минуту. Почему бы и «литературную» машину не пустить таким темпом? Словом, как видите, у меня идея Лассвица получает конструктивное воплощение и притом в довольно простой форме - длинного ряда шестеренок, насаженных на одну ось и вращаемых с большою (но технически осуществимою) скоростью.

Что мы должны думать об этом проекте «литературной» машины?

То, что он так же несбыточен, как и первоначальный проект Лассвица. Соорудить и пустить в ход эту «литературную» машину вполне возможно, но дождаться конца ее работы человечество не сможет. Солнце погаснет, вселенная успеет миллионы раз погибнуть и возродиться, прежде чем последняя шестеренка закончит свое вращение. Действительно, при 30.000 оборотах в секунду

* Для удобства подсчета принимаем год равным 360 суткам.

Надо ли продолжать? Если 12-я шестеренка начнет вращаться только через двести миллионов лет, то когда дойдет очередь до 1000-й? Нетрудно вычислить. Число минут выразится числом

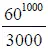
- числом, в котором 1775 цифр. Во всей вселенной не хватит материи, чтобы дать материал для всех оттисков, число которых выражается 1779 цифрами. Ведь во вселенной, по подсчетам специалистов (де-Ситтера), «всего» 10 77электронов, и даже если бы каждый оттиск состоял из одного электрона, можно было бы отпечатать лишь ничтожную долю всей продукции «литературной» машины. Перерабатывать старые оттиски вновь на бумагу? Но допуская даже при этом ничтожнейшую потерю материи в 1 биллионную долю, мы должны были бы иметь - считая снова по электрону на оттиск - число оттисков из 1767 цифр, а электронов у нас имеется число всего из 78 цифр…

Но можно возразить, пожалуй, что незачем ждать окончания работы «литературной» машины: ведь шедевры литературы и замечательные открытия могут случайно оказаться среди первого миллиона оттисков. При невообразимо огромном числе всех возможных сочетаний эта вероятность еще более ничтожна, чем вероятность случайно наткнуться на один определенный электрон среди всех электронов вселенной. Число электронов во вселенной неизмеримо меньше, чем общее число возможных оттисков нашей машины.

Но пусть даже осуществилось несбыточное, пусть случилось чудо, и в наших руках имеется сообщение о научном открытии, появившееся из-под машины без участия творческой мысли. Сможем ли мы этим открытием воспользоваться?

Нет, мы даже не сможем признать этого открытия. Ведь у нас не будет критерия, который позволил бы нам отличить истинное открытие от многих мнимых, столь же авторитетно возвещаемых в процессе работы нашей машины. Пусть, в самом деле, машина дала нам отчет о превращении ртути в золото. Наряду с правильным описанием этого открытия будет столько же шансов иметь множество неправильных его описаний, а кроме того, описаний и таких невозможных процессов, как превращение меди в золото, марганца в золото, кальция в золото и т. д. и т. д. Оттиск, утверждающий, что превращение ртути в золото достигается при высокой температуре, ничем не отличается от оттиска, предписывающего прибегнуть к низкой температуре, причем могут существовать варианты оттисков с указанием всех температур от минус 273° до бесконечности. С равным успехом могут появиться из-под машины указания на необходимость пользоваться высоким давлением (тысячи вариантов), электризацией (опять тысячи вариантов), разными кислотами (снова тысячи и тысячи вариантов) и т. п.

Как при таких условиях отличить подлинное открытие от мнимого? Пришлось бы тщательно проверять на опыте каждое указание (кроме, конечно, явно нелепых), т. е. проделать такую огромную лабораторную работу, которая совершенно обесценила бы всю экономичность идеи «литературной» машины.

Точно также пришлось бы проделать обширные исторические изыскания, чтобы проверить правильность каждого исторического факта, утверждаемого каким-нибудь продуктом механического производства открытий. Словом, в виду полной невозможности отличать истину от лжи, подобный «механический» способ двигать науку вперед был бы совершенно бесполезен, даже если бы каким-нибудь чудом удалось дождаться осмысленного оттиска.

Интересно отметить здесь следующий расчет Бореля (из книги «Случай»): вероятность выпадения орла 1000 раз подряд при игре в орлянку равна 1/ 21000, т. е. числу, знаменатель которого содержит около 300 цифр. Этот шанс приблизительно таков же, как и шанс получить две первых строки определенного стихотворения, вынимая наудачу из шапки буквы по следующему способу: в шапке 25 букв, одна из них вынимается, записывается и кладется обратно в шапку; после встряхивания вынимается вторая, и т. д. Строго говоря, получить таким образом две первых строки определенного стихотворения вполне возможно. «Однако, - замечает Борель, - это представляется нам до такой степени маловероятным, что если бы подобный опыт удался на наших глазах, мы считали бы это плутовством» [33].

Около полувека назад - в конце 70-х годов, - вынырнула в Соединенных Штатах одна игра, «игра в 15»; она быстро распространилась по всему цивилизованному миру и, благодаря несчетному числу усердных игроков, которых она заполонила, превратилась в настоящее общественное бедствие, в истинный бич человечества. Заглавный рисунок, заимствуемый из одного американского сочинения, изображает эту игру: коробку с 15 шашками, перенумерованными от 1 до 15, и одним свободным полем. Перед ящиком мы видим жертву игорной страсти, одного из многочисленных одержимых этой манией; в разгар полевой работы, он, поддавшись внезапно приступу игорной лихорадки, кинулся на колени перед демоном, которому поклонялся. Растерянность видна во всей его фигуре, во всех его чертах; лицо искажено отчаянием; правая рука нервно сжата в кулак; левая рука и наморщенный лоб охвачены судорогой. Кожа головы, после ряда усилий, скинула шляпу; волосы дико растрепаны. Забыт труд, покинута лошадь и плуг; на нем уселась пара птиц; даже заяц, обычно столь пугливый, сознает, что этот потерянный для мира маньяк, всецело погруженный в 15 шашек своей коробки, не представляет для него ни малейшей опасности.