Яков Перельман - Математика для любознательных

Премия в 1000 долларов, предложенная за первое правильное решение этой задачи, никем не была заслужена, хотя тысячи людей уверяли, что выполнили требуемое. Все принялись без устали решать эту задачу. Рассказывали забавные истории о торговцах, забывавших из-за этого открывать свои магазины, о почтенных чиновниках, целые ночи напролет простаивавших под уличным фонарем, отыскивая путь к решению. Непостижимой особенностью игры было то, что никто не желал отказываться от поисков решения, так как все чувствовали уверенность в ожидающем их успехе. Штурмана, говорят, из-за игры садили на мель свои суда, машинисты проводили поезда мимо станций, торговля была деморализована. Фермеры забрасывали свои плуги, и один из таких моментов изображен на прилагаемой иллюстрации.

Вот несколько новых задач, кроме той, которая приведена выше:

Задача 2-я. Исходя из расположения, показанного на схеме II, привести шашки в правильный порядок, но со свободным полем в левом верхнем углу (см. чертеж).

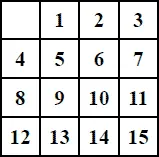
К задаче 2-й.

Задача 3-я. Исходя из расположения схемы II, поверните коробку на четверть оборота и передвигайте шашки до тех пор, пока они не примут расположения чертежа.

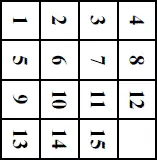
К задаче 3-й.

Задача 4-я. Передвижением шашек превратите коробку в «магический квадрат», а именно, разместите шашки так, чтобы сумма чисел была во всех направлениях равна 30.

Расположение зад. 2-й может быть получено из начального положения следующими 44 ходами.

14, 11, 12, 8, 7, 6, 10, 12, 8, 7,

4, 3, 6, 4, 7, 14, 11, 15, 13, 9,

12, 8, 4, 10, 8, 4, 14, 11, 15, 13,

9, 12, 4, 8, 5, 4, 8, 9, 13, 14,

10, 6, 2, 1.

Расположение зад. 3 достигается следующими 39 ходами:

14, 15, 10, 6, 7, 11, 15, 10, 13, 9,

5, 1, 2, 3, 4, 8, 12, 15, 10, 13,

9, 5, 1, 2, 3, 4, 8, 12, 15, 14,

13, 9, 5, 1, 2, 3, 4, 8, 12.

Магический квадрат с суммою 30 получается ряда ходов:

12, 8, 4, 3, 2, 6, 10, 9, 13, 15,

14, 12, 8, 4, 7, 10, 9, 14, 12, 8,

4, 7, 10, 9, 6, 2, 3, 10, 9, 6,

5, 1, 2, 3, 6, 5, 3, 2, 1, 13,

14, 3, 2, 1, 13, 14, 3, 12, 15, 3.

Приведем замечание немецкого математика Шуберта о числе возможных задач при «игре в 15».

«Сколько всего возможно задач; т. е. сколько различных расположений можно дать 15 шашкам, причем каждый раз пустое поле расположено справа внизу? Чтобы определить, сколько перестановок можно получить с помощью 15 предметов, начнем с 2-х предметов: а и b. Они могут дать лишь две перестановки, именно - ab и Ьа. При трех предметах имеется уже втрое больше перестановок, т. е. 6, так как предмет а может быть поставлен перед Ьс и перед cb, и кроме того, имеются еще две перестановки, начинающиеся с b, и две начинающиеся с с. Отсюда можно заключить, что четыре предмета а, b, с, d могут дать вчетверо большее число различных перестановок, т. е. 4x3x2 = 24 перестановки. Продолжая так, можно найти, что 15 шашек допускают всего

2x3x4x5x6x7x8x9x10x11x12x13x14x15

перестановок. Вычислив это произведение, мы найдем для числа задач игры внушительное число:

1 биллион 307674 миллиона 368000».

Из этого огромного числа задач ровно половина принадлежит к разрешимым и столько же - к неразрешимым. Заметим еще, что если бы возможно было ежесекундно давать шашкам новое положение, то чтобы перепробовать всевозможные расположения, потребовалось бы, при непрерывной работе круглые сутки, - свыше 40.000 лет.

Ряд лет тому назад в Берлине подвизался искусный счетчик, предлагавший публике такую задачу (переделываем ее на русский лад):

«Кто сможет уплатить 5 рублей, 3 рубля или 2 рубля полтинниками, двугривенными и пятаками, всего 20-ю монетами, - тому будет выдано наличными деньгами сто рублей».

Посетителям вручались необходимые монеты, - конечно, заимообразно. Но обещанная сотня рублей должна была остаться навсегда в руках счастливца, которому удалось бы решить задачу.

Разумеется, пол-Берлина потело над разрешением этой задачи (стояли как раз жаркие июльские дни), казавшейся не особенно трудной. Сто рублей хорошо пригодились бы всем, значит - стоит потрудиться. По мере того, как выяснялась бесполезность попыток, физиономии решавших вытягивались и розовые мечты о заманчивой награде испарялись. Надежды оказывались обманчивыми. Ловкий счетчик мог безбоязненно обещать в десять раз большую награду. Никто не в праве был бы на нее притязать, ибо задача требует невозможного.

Как в этом убедиться?

Нам не понадобится глубоко забираться в дебри алгебры, но все же не будем бояться х, у и z.

Рассмотрим сначала, можно ли уплатить требуемым образом пять рублей. Пусть для этого нужно х полтинников, у - двугривенных и z - пятаков. Сумма их должна составить 500 копеек, т. е.

50x + 20y + 5z = 500,

или, разделив на 5,

10x + 4y + z = 100.

Это легко осуществить на разные лады. Если, например, взять х = 8, то будем иметь

80 + 4y + z = 100,

или

4y + z = 20;

последнему уравнению можно удовлетворить, если принять z = 4, или 8, или 12, или 16 и, следовательно (при z = 4), 4у = 16, у = 4. Действительно, 8 полтинников, 4 двугривенных и 4 пятака составляют 500. Однако при этом не выполнено условие употребить в общей сложности 20 монет: мы употребили 8 + 4 + 4 = 16 монет. К нашему первому уравнению

10x + 4y + z = 100

необходимо, следовательно, присоединить второе

x + y + z = 20.

Соединяя их в одно, посредством вычитания второго из первого, мы освобождаемся от z и получаем

9х + 3у = 80;

теперь сразу становится очевидным, что не может быть таких целых чисел, которые удовлетворили бы этому уравнению. Потому что 9 раз х, каково бы ни было х, есть непременно число кратное 3; то же верно для числа 3у; следовательно, сумма 9х + 3у должна делиться без остатка на 3, то есть никак не может равняться 80.

Задача приводит к противоречивому требованию, и значит - ее решение невозможно.

Совершенно так же невозможно и составление требуемым образом сумм в 3 рубля и в 2 рубля. В первом случае, как каждый легко может убедиться, получается уравнение:

9х + 3у = 40;

во втором:

9x + 3y = 20.

Оба равенства невозможны, так как ни 40, ни 20 не делятся без остатка на 3.

Сказанным задача собственно исчерпывается. Но поучительно присоединить к ней рассмотрение вопроса, какие же суммы можно этими 20-ю монетами в самом деле уплатить, - разумеется так, чтобы получилось целое число рублей.

Если обозначим это число рублей через т, то у нас будет уравнение

50x + 20y + 5z = 100m,