Стивен Строгац - Удовольствие от Х.Увлекательная экскурсия в мир математики от одного из лучших преподавателей в мир

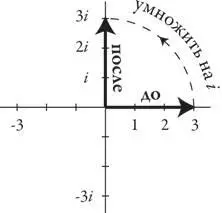
Таким образом, умножение на i представляет собой вращение против часовой стрелки на четверть оборота. До умножения на i число 3 обозначается стрелкой длиною 3, направленной на восток, результатом умножения на i будет стрелка такой же длины, но направленная на север.

Инженеры-электротехники любят комплексные числа именно по этой причине. Иметь такой компактный способ представления вращения на 90° при работе с переменным током, напряжением или электрическими и магнитными полями очень удобно, потому что они часто связаны с колебаниями или волнами, которые составляют четверть цикла (то есть представляют сдвиг фазы на 90°).

Действительно, комплексные числа необходимы всем инженерам. В авиационно-космической промышленности они облегчили расчеты подъема крыла самолета. Инженеры-строители и инженеры-механики регулярно используют их для анализа вибрации элементов пешеходных мостов, небоскребов и автомобилей на ухабистой дороге.

Поворот на 90° также проливает свет на то, что на самом деле означает i 2= –1. Если мы умножим положительное число на i 2, то стрелка, равная длине положительного числа, повернется на 180° в направлении с востока на запад, так как производится два поворота на 90° (по одному для каждой степени i ), в итоге — на 180°.

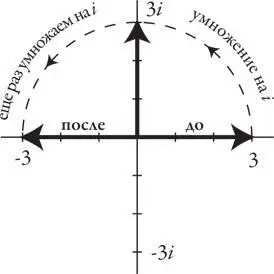
Но умножение на –1 делает такое же сальто на 180°. Вот поэтому i 2= –1.

Компьютеры вдохнули новую жизнь в комплексные числа и вековую проблему извлечения корней. Когда ПК не используются нами для веб-серфинга или отправки и получения электронной почты, они на наших столах способны обнаружить такое, что древние и представить себе не могли.

В 1976 году мой коллега по Корнуолльскому университету Джон Хаббард попытался применить в задачах по динамике метод Ньютона [40] Прекрасную журналистскую работу о Джоне Хаббарде можно найти в книге J. Gleick, Chaos, р. 217 (Viking, 1987). Собственный взгляд Хаббарда на метод Ньютона отображен в разделе 2.8 книги J. Hubbard and B. B. Hubbard, Vector Calculus, Linear Algebra, and Differential Forms, 4 th edition (Matrix Editions, 2009). Для читателей, которые хотят углубиться в математический аппарат метода Ньютона, более сложное, но все же довольно понятное объяснение дано в книге H.-O. Peitgen and P. H. Richter, The Beauty of Fractals (Springer, 1986), chapter 6; также см. статью Эдриана Двади (сотрудник Хаббарда), озаглавленную Julia sets and the Mandelbrot set, в этой же книге. , мощный алгоритм для поиска корней уравнений в комплексной плоскости. В соответствии с этим методом выбирается начальное значение (близкое к значению корня) и неоднократно производятся определенные вычисления. При этом на каждом последующем шаге используется значение, полученное на предыдущем. Этот метод позволяет быстро приблизиться к корням уравнения.

Хаббард заинтересовался множественными корнями. Какой из множественных корней можно найти методом Ньютона? Хаббард доказал, что из двух корней всегда будет найден тот, который наиболее близок к начальному значению. Однако при наличии трех и более корней его предыдущее доказательство не сработало.

Тогда Хаббард провел так называемый численный эксперимент . Он запрограммировал компьютер на выполнение метода Ньютона, настроив устройство так, чтобы оно маркировало цветом миллионы различных начальных значений в соответствии с тем, к какому корню они приближались, и меняло интенсивность цвета в зависимости от скорости их приближения к корню.

До того как Хаббард увидел результат, он предполагал, что к корням уравнения быстрее всего притянутся наиболее близкие к ним по значению, и это отобразится в виде ярких точек на сплошном цветовом пятне. Но вот границы между пятнами? О них он даже не думал.

Компьютер выдал неожиданный результат.

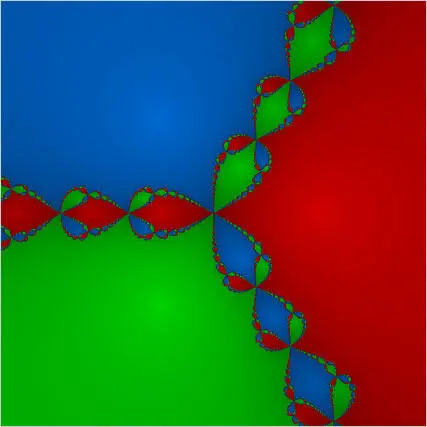
Пограничная область между пятнами напоминала психоделические галлюцинации [41] Хаббард не был первым математиком, поставившим вопрос о применении метода Ньютона, в комплексной плоскости. Артур Кэли, британский математик, задал его еще в 1879 году. Он также рассмотрел квадратичный и кубический полиномы и понял, что первый случай гораздо проще, чем второй. Хотя тогда он еще не мог знать о фракталах, которые были обнаружены век спустя, он прекрасно понимал, что есть риск возникновения определенных проблем, если корней окажется больше двух. В его небольшой (на одну страницу) статье Desiderata and suggestions: No.3—the Newton-Fourier imaginary problem, American Journal of Mathematics, 2(1), March 1879, p. 97, с которой можно ознакомиться на сайте http://www.jstor.org/pss/2369201, заключение звучит как сдержанное предупреждение: «Для квадратного уравнения решение легко и элегантно, но представляется, что решение кубического уравнения окажется значительно сложнее». . Цвета в ней смешивались беспорядочно, соприкасаясь друг с другом в невероятно большом количестве точек. Они всегда располагались в трех направлениях. Другими словами, где бы ни появлялись два цвета, между ними всегда присутствовал третий.

Расширение границ выявило наличие пятен внутри пятна.

Структура была фрактальной [42] Снимки, представленные в этой главе, были рассчитаны методом Ньютона, примененного для нахождения корней многочлена z 3 — 1. Его корни — три кубических корня из 1. Для этого случая в соответствии с алгоритмом Ньютона на комплексной плоскости выбирается точка z , она и переносит значение корня в новую точку, рассчитанную по формуле z — ( z 3 — 1)/(3 z 2 ). Именно это значение и становится следующим значением z . Данный процесс повторяется, пока z не подходит достаточно близко к корню или, что эквивалентно, пока z 3 — 1, не подойдет достаточно близко к нулю, где под «достаточно близко» понимается очень маленькое расстояние, выбранное программистом. Затем все исходные точки, которые приводят к определенному корню, окрашиваются в одинаковый цвет. Таким образом, точки красного цвета сходятся к одному корню, точки зеленого — к другому, а синего — к третьему. Снимки окончательного фрактала Ньютона были любезно предоставлены Саймоном Татемом. Дополнительные сведения о его работе вы найдете на странице Fractals derived from Newton-Raphson iteration на сайте: http://www.chiark.greenend.org.uk/~sgtatham/newton/. Видеоанимация фрактала Ньютона сделана Teamfresh. Потрясающе глубокое масштабирование других фракталов, в том числе знаменитого множества Мандельброта, можно увидеть на сайте Teamfresh по адресу http://www.hd-fractals.com. — сложной формы, внутренняя структура которой повторялась во все более мелких масштабах.