Стивен Строгац - Удовольствие от Х.Увлекательная экскурсия в мир математики от одного из лучших преподавателей в мир

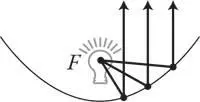
Когда вы оцените фокусирующую способность парабол и эллипсов, то удивитесь, что среди всех геометрических фигур больше практически ни одна не обладает подобными свойствами. Не лежат ли в их основе какие-то фундаментальные закономерности?

У математиков и сторонников теории заговора [67] Теория заговора — взгляд на некоторые общественно-значимые события или ход истории в целом как на результат заговора со стороны определенной группы людей, управляющих этим процессом из корысти, амбиций или иных интересов. Прим. ред. много общего: мы не доверяем совпадениям, особенно удачным. Отрицаем случайности. Все имеет свою причину. Применительно к реальной жизни такой способ мышления, возможно, кажется несколько параноидальным, но для математика он совершенно нормален. В идеальном мире чисел и фигур странные совпадения обычно являются ключами к тому, чего мы не замечаем, и свидетельствуют о наличии скрытых закономерностей.

Итак, рассмотрим более подробно возможную связь между параболами и эллипсами [68] Информацию о конических сечениях и ссылки на обширную литературу о них см. http://mathworld.wolfram.com/ConicSection.html и http://en.wikipedia.org/wiki/Conic_section. Прим. ред.: О конических сечениях популярно: И. Н. Бронштейн. Общие свойства конических сечений // Квант. 1975. № 5. О конических сечениях для читателей с математической подготовкой: Акопян А. В., Заславский А. А. Геометрические свойства кривых второго порядка. М.: МЦНМО, 2007. . На первый взгляд, они не похожи. Параболы имеют форму арки, вытянутой на обоих концах. У эллипсов овальная форма, и они напоминают раздавленные окружности, замкнутые и ограниченные.

Но как только вы выйдете за рамки стандартных представлений и исследуете анатомию этих фигур, то заметите, насколько они похожи. Обе принадлежат к королевской семье кривых; генетическая связь между ними становится очевидной, когда понимаешь, куда нужно смотреть.

Чтобы объяснить, как они связаны между собой, необходимо вспомнить, что в точности означают эти кривые.

Парабола обычно определяется как множество всех точек, равноудаленных от данной точки и данной прямой, не содержащей эту точку. Это труднопостигаемое толкование, но его довольно легко понять, если представить следующую картинку, при этом обозначив данную точку F как фокус, а прямую как L .

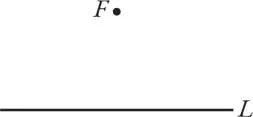
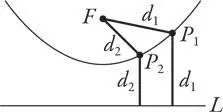
В соответствии с определением парабола состоит из всех точек, которые лежат на одинаковом расстоянии от F и L . Например, точка Р , находящаяся прямо под F на полпути к L , точно подходит под это определение.

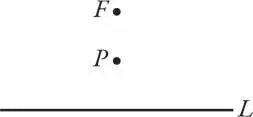
Бесконечное множество других точек P 1, P 2… тоже подходят под него, как показано ниже.

>

Точка P 1расположена на одинаковом расстоянии d 1от прямой и фокуса. То же самое верно и для точки P 2, но в этом случае имеется в виду некое расстояние d 2. Все точки P с таким свойством образуют данную параболу.

Почему мы считаем F фокусом, становится ясно, если представить параболу как кривое зеркало. Оказывается (хотя я не стану это доказывать), если направить луч света прямо на параболическое зеркало [69] Вы сможете дать разгуляться своей интуиции, наблюдая за онлайн-анимацией, созданной Лу Талманом, и обсудить свои идеи на его странице The geometry of the conic sections («Геометрия конических сечений»). , все отраженные лучи пересекутся в одной точке F , создавая сильно сфокусированное пятно света.

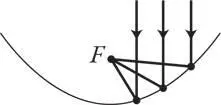
По такому же принципу работали старые лампы для загара, под которыми предыдущее поколение жарилось в те далекие времена, когда никто не беспокоился о раке кожи.

Теперь давайте обратимся к эллипсу. Он определяется как множество точек, для которых сумма расстояний от двух данных точек является константой. Если перевести это на простой язык, получим инструкцию, как нарисовать эллипс. Возьмите ручку, лист бумаги, чертежную доску, две канцелярские кнопки и кусочек веревки. Положите бумагу на доску. Несильно ее натягивая, прикрепите к ней концы веревки канцелярскими кнопками. Затем зацепите веревку карандашом и натяните ее, образуя угол, как показано ниже. Когда начнете рисовать, следите за тем, чтобы веревка все время была натянута. Начинайте вести карандашом по бумаге вокруг кнопок и, сделав полный круг, получите эллипс.

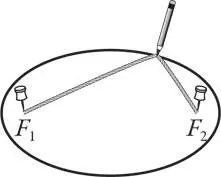
Линия, полученная в результате, полностью соответствует определению эллипса. Кнопки играют роль двух заданных точек. А сумма расстояний от них до любой точки на кривой всегда постоянна независимо от положения карандаша, потому что неизменно совпадает с длиной веревки.

Где же в этой конструкции фокусы эллипса? Там, где находятся кнопки. Я не буду это доказывать, но именно фокусы позволяют Люку и Дарту все время попадать в противника и загоняют шар в лузу при игре в бильярд на эллиптическом столе.

Вопрос: почему именно параболы и эллипсы имеют такую фантастическую способность фокусировать? Каким секретом они обладают?

Ответ: оба представляют собой поперечные сечения конуса.

Конус? Вы, возможно, не понимаете, причем тут он, но это именно то, что нам нужно. Просто до сих пор роль конуса была скрыта от нас.

Чтобы понять, причем здесь конус, представьте себе, как вы разрубаете его тесаком для разделки мяса, как если бы нарез а ли салями косо со все более увеличивающимся углом наклона ножа. Если конус разрезать горизонтально, то его сечением будет окружность.

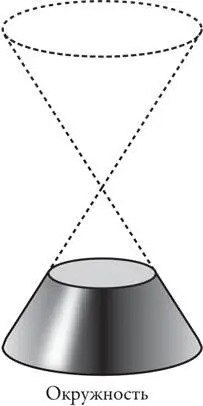
Но если разрезать конус под небольшим наклоном, то его сечение из окружности превращается в эллипс.

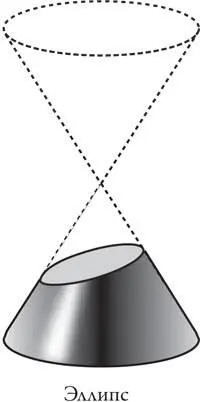
Чем больше угол наклона сечения, тем длиннее и тоньше пропорции эллипса. И при критическом угле, равном углу наклона образующей конуса, эллипс превращается в параболу.