Роза Мария Рос - Мир математики. т.30. Музыка сфер. Астрономия и математика

* * *

МАСШТАБНЫЕ МОДЕЛИ СОЛНЕЧНОЙ СИСТЕМЫ

Как мы уже говорили, представить себе истинные размеры Солнечной системы непросто. Чтобы получить более четкое представление о них, изготовим простую модель. Лучше всего сделать макет, в котором планеты Солнечной системы будут представлены в масштабе на соответствующих расстояниях друг от друга. Основная проблема заключается в том, что очень сложно подобрать масштаб, при котором планеты будут не слишком мелкими, а расстояния между ними — не слишком большими.

Будем использовать в качестве моделей планет мячи разного размера. Поместим на одном краю парка или площади гандбольный мяч примерно 25 см в диаметре, который будет обозначать Солнце. Меркурий будет обозначать булавочная головка (1 мм в диаметре), расположенная в 10 метрах от Солнца. Еще одна булавочная головка большего размера (2 мм в диаметре) на расстоянии 19 метров от Солнца будет обозначать Венеру. Земля будет еще одной булавочной головкой (2 мм в диаметре) в 27 метрах от Солнца. Марс вновь будет представлен булавочной головкой (1 мм в диаметре) в 41 метре от Солнца. Шарик для пинг-понга (2,5 см в диаметре) — это модель Юпитера. Он будет находиться на расстоянии 140 метров от Солнца.

Еще один шарик диаметром 2 см в 250 метрах от Солнца будет изображать Сатурн. Модель Урана — стеклянный шарик диаметром 1 см на расстоянии 500 метров от Солнца. И наконец, еще один стеклянный шарик диаметром 1 см в 800 метрах от Солнца будет обозначать Нептун.

Планеты, в отличие от нашей модели, не лежат на одной прямой, а движутся по своим орбитам, и, следовательно, расстояние между ними будет еще больше.

* * *

Могут ли столкнуться две планеты?

Этот вопрос часто задают дети, когда им рассказывают о Солнечной системе. Но, как вы видите, в космосе достаточно места. Чтобы две планеты сошли с орбит, необходимо действие третьего небесного тела огромнейших размеров, которое вызовет значительное гравитационное возмущение. Вероятность такого события очень мала.

Намного вероятнее столкновение с планетами астероидов или комет. Так, Аризонский кратер, самый известный из всех кратеров Земли, появился после столкновения метеорита с Землей. Луна испещрена кратерами, так как ее атмосфера слишком разрежена, в то время как в атмосфере Земли большинство небесных тел сгорает еще до столкновения с поверхностью. От столкновений с небесными телами страдают и другие планеты: в июле 1994 года комета Шумейкер-Леви 9, расколовшись на 21 часть, вошла в атмосферу Юпитера и ударилась о его поверхность.

Результаты этого столкновения можно было наблюдать с Земли. Очевидно, что в те времена, когда Солнечная система только формировалась, подобные случаи происходили намного чаще.

Небесная механика способна описать траектории планет и предсказать их всевозможные астрономические транзиты и относительные положения. Для составления подобных прогнозов используются элементы орбит небесных тел Солнечной системы. Расскажем о них на примере планет. Элементы орбит подобны штрихкоду, так как содержат всю необходимую информацию для точного расчета орбит планет.

Элементы орбит планет, или кеплеровы элементы, первым определил Иоганн Кеплер. Он же начал применять их для изучения движения планет вокруг Солнца.

Созданные им методы вычислений позднее легли в основу расчетов Ньютона, Гаусса, Лапласа и Ольберса. Хотя далее мы подробно расскажем об элементах орбит планет, в действительности они используются при изучении орбит любых небесных тел, будь то планеты, астероиды, кометы, искусственные спутники и любые другие тела, имеющие массу.

Элементы орбиты планеты — это шесть величин, позволяющие в точности определить орбиту движения планеты вокруг Солнца, которое находится в одном из фокусов этой орбиты. Первые три элемента — это так называемые эйлеровы углы, с помощью которых задаются положения планеты в пространстве. Три остальных элемента описывают форму орбиты и положение планеты на ней. Эти шесть элементов орбиты таковы: долгота восходящего узла Ω , наклонение i , аргумент перицентра ω , большая полуось а , эксцентриситет е и средняя аномалия M о . Рассмотрим подробнее три последние величины, которые определяют форму и размер эллиптической орбиты и положение планеты на ней.

Большая полуось орбиты а — это половина большой оси эллипса. Ближайшая к Солнцу точка пересечения большой полуоси с орбитой называется перигелием, наиболее удаленная от Солнца — афелием (см. рисунок). Таким образом, расстояние между перигелием и афелием равно удвоенной большой полуоси эллипса.

Определить размер эллипса можно и другим способом: для этого нужно заменить большую полуось на период вращения, то есть время, за которое планета совершает полный оборот вокруг Солнца. Любая из этих двух величин дает нам представление о размерах орбиты.

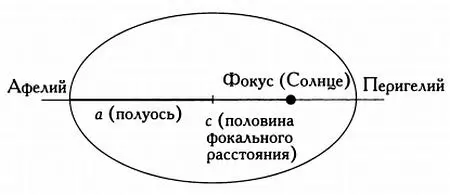
Орбита планеты имеет форму эллипса. На схеме отмечены большая полуось, половина фокального расстояния, афелий и перигелий. В фокусе эллипса находится Солнце. Эксцентриситет рассчитывается по формуле е = с/а.

Эксцентриситет эллипса е указывает, насколько вытянут эллипс. Эксцентриситет определяется как половина расстояния между фокусами с, разделенная на длину большей полуоси эллипса а, то есть е = с/а. Если бы орбита планеты имела форму окружности, оба фокуса совпали бы в ее центре, расстояние между фокусами было бы равно нулю, следовательно, эксцентриситет также равнялся бы нулю.

Если эксцентриситет орбиты очень мал и практически равен нулю, орбита по форме близка к окружности — именно такую форму имеют орбиты большинства планет.

Эксцентриситет эллипса всегда меньше 1, так как половина фокального расстояния всегда меньше большой полуоси.

Когда эксцентриситет равен 1, эллипс приобретает форму параболы — незамкнутой кривой — и не описывает орбиту какой-либо из планет. Если рассматривать орбиты комет, то их эксцентриситет может быть даже больше 1 — в этом случае орбита будет иметь форму гиперболы. В подобных случаях кометы приближаются к Солнцу лишь однажды, после чего, пройдя через перигелий, больше никогда не возвращаются в Солнечную систему. Такие кометы выглядят намного эффектнее, чем кометы, движущиеся по эллиптическим орбитам: последние периодически приближаются к Солнцу и при каждом прохождении мимо него теряют часть своей массы, пока не будут уничтожены совсем. Определить положение небесного тела на орбите можно в момент, когда она проходит через перигелий.