Роза Мария Рос - Мир математики. т.30. Музыка сфер. Астрономия и математика

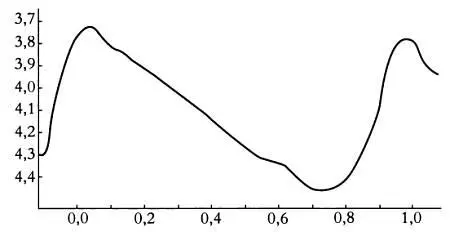
Кривая блеска Дельты Цефея.

При каждом наблюдении нужно определить видимую величину переменной звезды путем сравнения с двумя другими звездами А и В . Этот метод называется методом Аргеландера. Очевидно, что звезды А и В , фигурирующие в сравнении, должны быть постоянными, а их величина должна быть известна. Желательно, чтобы эти звезды имели тот же цвет, что и рассматриваемая звезда. Обозначим видимые величины этих звезд через m А и m B , где m А > m B . Введем обозначения Аа и ЬВ , где значения а, Ь = 1, 2, 3, 4 и 5 и определяются по следующим правилам:

— А1: имеются некоторые сомнения относительно блеска звезды А и переменной звезды (они почти одинаковы);

— А2: имеются некоторые сомнения, однако звезда А ярче, чем переменная звезда;

— АЗ: величины звезд сопоставимы, но звезда А очевидно ярче;

— А4: сразу же видно, что звезда А ярче;

— А5: звезда А , вне всяких сомнений, ярче;

— 1В: имеются некоторые сомнения относительно блеска звезды В и переменной звезды (они почти одинаковы);

— 2В: имеются некоторые сомнения, однако звезда В не столь яркая, как переменная звезда;

— 3В: величины звезд сопоставимы, но звезда В очевидно менее яркая;

— 4В: сразу же видно, что звезда В менее яркая;

— 5В: звезда В , вне всяких сомнений, менее яркая.

По этим правилам можно определить а и Ь для каждого наблюдения и вычислить видимую величину переменной звезды по формуле:

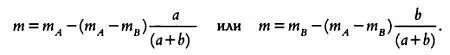
Так определяется величина звезды — первая координата точки ( m, р ) на кривой блеска.

Чтобы найти вторую координату, нужно определить фазу р переменной звезды в момент наблюдения. Она определяется с учетом дня, часа и минуты наблюдений, выраженных в юлианских днях D . Эфемерида Е позволяет определить момент, когда звезда блестит ярче всего (также указывается юлианский день). Нужно определить период изменения блеска звезды Р . Если мы вычислим

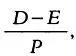
получим десятичную дробь. Ее целая часть укажет число максимумов, наблюдавшихся с эфемериды Е до момента наблюдения D . Для построения кривой это число не будет особенно полезным. Нас интересует дробная часть полученного результата, то есть фаза переменной звезды в момент наблюдения:

Юлианский день может соответствовать любой дате, однако, в отличие от нашего календаря, юлианские дни отсчитываются непрерывно. Ввиду множества реформ календаря и других особенностей, в частности отсутствия нулевого года и существования високосных годов, подсчитать число дней между двумя событиями непросто. К примеру, папа Григорий XIII исключил из календаря 10 дней: за 4 октября 1582 года последовало 15 октября того же года. Как видите, определение длительных временных интервалов по нашему календарю может оказаться очень сложным.

В 1582 году Жозеф Скалигер определил непрерывный календарь, который начинался 1 января 4713 года до н. э. в 12 часов дня (в то время сутки начинались в полдень, в момент прохождения Солнца через меридиан места, а не в полночь, как сейчас).

Дни в этом календаре отсчитывались без промежутков и назывались юлианскими. К примеру, полдень 1 января 2010 году — это юлианский день 2 455198.

BROMAN, L., ESTALELLA, R., Ros, R.M., Experimentos de Astronomia, Mexico D.F., Ed. Alhambra, 1997.

FlERRO, J ., Como acercarse a la astronomia, Mexico D.F., Ed. Limusa, 1997. —: Los mundos cercanoSy Mexico D. F., Me Graw Hill, 1997.

FlERRO, J., Ros, R.M., De planetasf estrellas у universos, Barcelona, Ed. Antares, 2009.

GALADf, D., Astronomia general: teoria у practica, Barcelona, Omega, 2001.

IBANEZ, R. et al., Divulgar las matematicas, Madrid, Ed. Nivola, 2005.

MORENO, M., Jose, J., De King Kong a Einsteint Barcelona, UPC, Col. Politext, 1999.

MORENO, R. Experimentos para todas las edades, Madrid, Ed. Rialp, 2008. —: Historia breve del Universo, Madrid, Ed. Rialp, 1998.

PASACHOFF, J., Astronomy: From the Earth to the Universe, Belmont, Brooks/Cole Publishing, 2002.

PUIG, LI., Ros, R.M., El robirobaty Vic, Eumo Ed., 2006.

ROS, R.M., Las gafas del Universo, Barcelona, Antares Ed., 2008. —: «Astronomy and Mathematics», Teaching and Learning Astronomy, Cambridge University Press, 2005. —: «The Transit of Venus: an Opportunity to Promote Astronomy», Teaching and Communicating Astronomy у Granada, EDP Sciences, 2005.

ROS, R.M., VlNUALES, E., Movimientos astronomicoSy Zaragoza, Mira Ed., 2003.

SAGAN, C., Cosmosу Barcelona, RBA Editores, 1980.

* * *

Перевод Б. Заходера . — Примеч. ред .