Роза Мария Рос - Мир математики. т.30. Музыка сфер. Астрономия и математика

В 1989 году была открыта группа галактик под названием Великая Стена, удаленная на расстояние более 500 млн световых лет, имеющая 200 млн световых лет в ширину и всего 15 млн световых лет в глубину. В 2004 году было открыто еще одно пустое суперпространство в созвездии Эридана, известное как Реликтовое холодное пятно, или Суперпустота Эридана, расположенное на расстоянии почти 1 млрд световых лет от нас. Существует множество других примеров, подтверждающих, что Вселенная имеет пузырьковую структуру.

Результаты этих наблюдений следует использовать с осторожностью. Необходимо учитывать, что они могут содержать ошибки, а многое на самом деле происходит вовсе не так, как нам кажется. С помощью гравитационных линз мы можем видеть астрономические объекты вовсе не там, где они находятся на самом деле.

Сегодня астрономы работают над тем, чтобы получить изображения огромных участков звездного неба, которые помогут лучше понять эволюцию Вселенной. Для достижения значимых результатов необходимы очень большие выборки. Изучением устройства Вселенной занимаются несколько групп исследователей, которые с помощью новой информации смогут улучшить модели, применяемые сегодня.

Преобразование азимутальных и экваториальных координат производится по правилам сферической тригонометрии. В современной математике эти преобразования координат описываются матрицами преобразований.

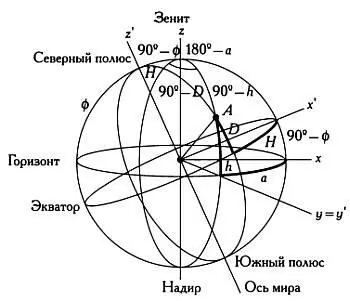
На иллюстрации положение звезды Аопределяется вектором, три составляющие которого определяются проекциями звезды на плоскость горизонта (плоскость ху ) и ось зенит — надир (ось z ). Таким образом, положение звезды задается тремя координатами: х, у, z . Следовательно, в горизонтальных координатах положение звезды Аможно определить как вектор ( r ∙ cos(h) ∙ cos(a), r ∙ cos(h) ∙ sin(a), r ∙ sin(h) ).

Аналогично определяется положение звезды относительно небесного экватора (плоскости х’у’ ) и оси мира (оси z’ ), то есть осей экваториальных координат х’ у’ z’ : ( r ∙ cos(D) cos(H), r ∙ cos(D) ∙ sin(H), r ∙ sin(D) ). Как показано на предыдущем рисунке, мы можем перейти от координат х, у, z к координатам х’ у’ z’ всего лишь выполнив поворот относительно оси у у которая совпадает с осью у’ на угол (90° — ф ), где ф — широта. В результате х перейдет в ось х’ ось z — в ось z . Матрица преобразований относительно второй оси (оси у = у’ ) для угла (90° — ф ) записывается так:

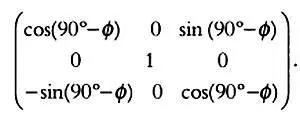
Имеем:

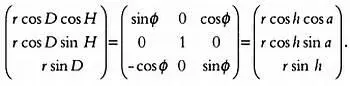
Следовательно, формулы преобразования координат записываются так:

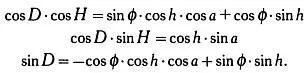
Те же соотношения, что выводятся с помощью матрицы преобразований, можно получить по формулам сферической тригонометрии Бесселя, рассмотрев треугольник «полюс-зенит-звезда», изображенный на иллюстрации на следующей странице.

На протяжении многих лет астрономы использовали этот треугольник для вычисления положения звезд. Так как ранее в их распоряжении не было ни компьютеров, ни других вычислительных машин, инструментами служили логарифмы и логарифмические таблицы. В этих таблицах приводились значения логарифмов для тригонометрических функций, аргументы которых выражались в градусах, минутах и секундах. Сферический треугольник «полюс-зенит-звезда» по-прежнему широко используется в сферической, или позиционной, астрономии, так как он содержит всю информацию, представленную на иллюстрации на предыдущей странице. Следует учитывать, что сторонами этого треугольника являются дуги большого круга небесной сферы. Следовательно, их длина измеряется в градусах, однако, по традиции, часовой угол и прямое восхождение отсчитываются в часах, минутах и секундах. Перейти от часов к градусам очень просто — достаточно учесть, что 360° эквивалентны 24 часам, или, что аналогично, 15° эквивалентны 1 часу.

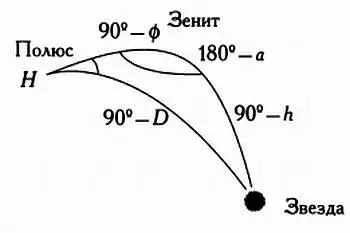
Треугольник полюс — зенит — звезда.

Аристарх Самосский(310 год до и. э. — 230 год до н. э.) определил отношения между расстояниями и радиусами небесных тел в системе «Земля — Луна — Солнце». Он вычислил отношение между радиусом Солнца и радиусом Луны, между расстоянием от Земли до Солнца и расстоянием от Земли до Луны, а также определил отношение радиуса Земли ко всем этим расстояниям. К сожалению, исследователь не смог рассчитать значение радиуса нашей планеты и вычислить абсолютные значения всех остальных радиусов и расстояний. Радиус Земли определил Эратосфен несколько лет спустя. Применив современную нотацию (и современные значения), мы покажем, как действовал Аристарх Самосский, и предложим читателю повторить его эксперимент. Вы убедитесь, что, проведя необходимые наблюдения, нетрудно получить те же результаты, что и древний мыслитель.

Отношение расстояний между Землей и Луной и Землей и Солнцем Аристарх Самосский определил, что угол, под которым с Земли виден отрезок, соединяющий Солнце и Луну, когда Луна находится в первой четверти, равен 87°.

Сегодня мы знаем, что он допустил ошибку — возможно, потому, что определить точный момент, когда Луна находится в первой четверти, очень сложно. Реальное значение этого угла равно 89°51’, в остальном же метод Аристарха Самосского полностью корректен. Обозначим через TS расстояние от Земли до Солнца, через TL — расстояние от Земли до Луны. Так как sin (9’) = TL / TS , имеем:

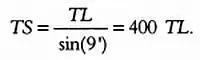
Аристарх Самосский вычислил, что TS = 19 TL .

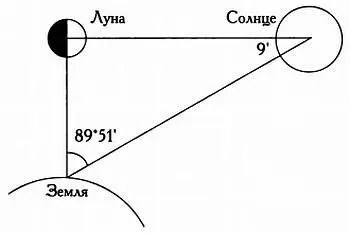
Расположение Луны в первой четверти относительно Земли и Солнца.

Отношение между радиусом Луны и Солнца

Отношение между радиусом Луны и Солнца должно рассчитываться по формуле, похожей на указанную выше, так как при наблюдении с Земли диаметры Луны и Солнца равны 0,5°. Следовательно, выполняется соотношение: