Роза Мария Рос - Мир математики. т.30. Музыка сфер. Астрономия и математика

Экспедиции в Вардё и Папеэте были организованы английскими учеными. Участники первой экспедиции отправились в Тихий океан, чтобы наблюдать прохождение Венеры по диску Солнца с острова Таити. Наблюдения провел Чарльз Грин и его заместитель, в то время никому не известный Джеймс Кук. Участниками второй экспедиции были глава Венской обсерватории святой отец Максимилиан Хелл, датский астроном Педер Хорребоу и юный англичанин Боргрюинг. Они направились в Вардё, на северо-западную оконечность Норвегии, где смогли наблюдать прохождение Венеры по диску Солнца во время полярного дня. Таким образом, ученые получили результаты наблюдений из двух точек одного меридиана, удаленных друг от друга на огромное расстояние.

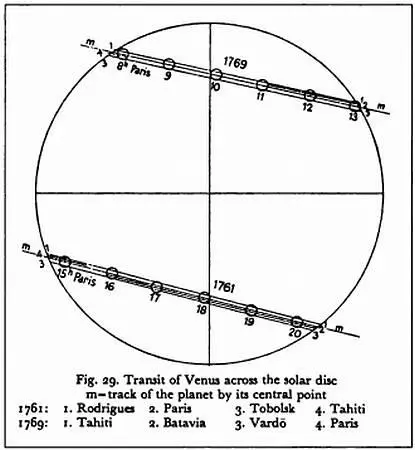
Результаты наблюдений прохождения Венеры по диску Солнца 3 июня 1769 года, опубликованные в «Истории астрономии» Антона Паннекука.

Как мы уже объясняли, с помощью параллакса можно вычислить расстояния между планетами, зная величины углов и референсное расстояние. При наблюдении прохождения Венеры по диску Солнца можно определить параллакс Венеры и Солнца и вычислить расстояние между Солнцем и Землей. Для этого проще всего наблюдать прохождение Венеры из двух достаточно далеких друг от друга точек земной поверхности. Измерив время прохождения в обоих случаях, можно рассчитать требуемые параллаксы и расстояние от Земли до Солнца.

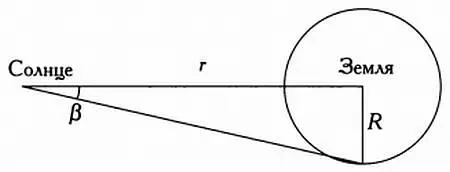
β— параллакс Солнца, или угол, под которым виден радиус Земли при наблюдении с Солнца.

Параллакс Солнца — это угол ( β , изображенный на предыдущем рисунке.

По определению тангенса, имеем

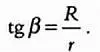
Так как величина угла очень мала, его тангенс примерно равен самому углу, выраженному в радианах. Выразив расстояние от Земли до Солнца, r, получим:

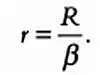
Для наблюдения этого параллакса мы должны находиться на Солнце, что невозможно. Наблюдатели располагаются в разных точках земной поверхности и смотрят на Солнце с Земли. Они видят прохождение Венеры по диску Солнца по-разному — точно так же мы видим один и тот же предмет немного по-разному, когда смотрим на него отдельно правым и левым глазом.

Рассмотрим двух наблюдателей, которые располагаются в точках A и В одного меридиана (с целью упрощения расчетов) на разных широтах. Они видят Венеру как точку (или маленький круг) на диске Солнца в двух разных положениях, А’ и В’ . Сравнив результаты этих двух наблюдений (см. следующий рисунок), мы сможем измерить смещение: расстояние А’В’ соответствует расстоянию между видимыми положениями Венеры при одновременном наблюдении из точек А и В .

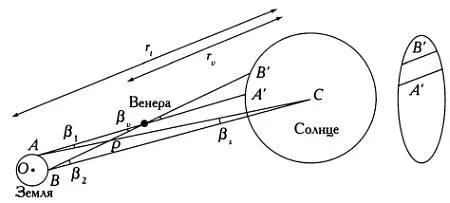
По результатам наблюдений за движением Венеры в течение транзита можно изобразить на диске Солнца ее траекторию. Если мы ведем наблюдения из точек А и В , получим две параллельные линии. Расстояние между ними будет параллаксным смещением Δβ , которое в любой момент времени будет соответствовать расстоянию А’В’ . Чтобы упростить расчеты, будем считать, что центры Земли ( О ), Венеры ( V ) и Солнца ( С ), а также точки земной поверхности А и В , из которых ведется наблюдение, расположены в одной плоскости. Углы при вершине Р в треугольниках APV и ВРС равны как вертикальные. Так как сумма углов любого треугольника равна 180°, выполняется следующее соотношение:

β v + β 1 = β s + β 2

Введем угол Δβ , которым обозначим расстояние между различными положениями Венеры на диске Солнца (оно будет равно расстоянию А’В’ в любой момент времени). Изменив порядок слагаемых, получим:

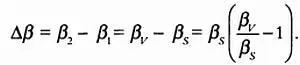
По определению, параллакс Венеры равен:

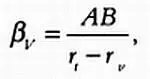
параллакс Солнца равен

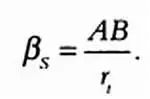
Подставив эти выражения в приведенное выше уравнение, получим:

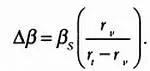
В частности, параллакс Солнца β s будет рассчитываться так:

где Δβ — расстояние между двумя траекториями Венеры, видимыми из различных точек земной поверхности, а отношение r t / r v можно рассчитать по третьему закону Кеплера. Куб этого отношения должен быть пропорционален квадрату отношения периодов обращения планет вокруг Солнца. Периоды обращения Венеры и Земли известны и равны 224,7 дня и 365,25 дня соответственно. Таким образом, параллакс Солнца β s удовлетворяет соотношению:

β s = 0,38248 Δβ .

Δβ определяется на основе результатов наблюдений из точек А и В , находящихся на одном меридиане. Мы используем рисунок XVIII века, на котором изображена траектория Венеры, видимая из разных точек одного меридиана при транзите.

Рассчитать Δβ можно разными способами:

1. Простейший способ — непосредственное измерение по рисунку, приведенному на странице 159: достаточно рассмотреть отношение диаметра Солнца D на рисунке и угловой размер Солнца. Угловой размер Солнца равен 30 минутам дуги, выраженным в радианах. Имеем:

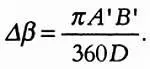
2. Также можно измерить хорды окружности на рисунке. Этот способ точнее, так как измерить длины хорд A 1A 2 и В 1В 2 всегда можно с большей точностью, чем расстояние между этими хордами А’В’ .

Рисунок позволяет связать длины хорд A 1A 2и В 1В 2с расстоянием между ними, А’В’.

По теореме Пифагора для треугольников SB’В 1 и SA’X 1 получим

3. Вместо расстояний можно отсчитывать время. Достаточно рассмотреть соотношение