Роза Мария Рос - Мир математики. т.30. Музыка сфер. Астрономия и математика

R s = 400 R l .

Отношение между расстоянием от Земли до Луны и радиусом Луны или между расстоянием от Земли до Солнца и радиусом Солнца

Так как диаметр Луны при наблюдении с Земли равен 0,5°, отложив его 720 раз, можно полностью покрыть орбиту Луны (предполагается, что она имеет форму окружности). Длина ее орбиты в 2 π раз больше расстояния от Земли до Луны, то есть 2 R L ∙ 720 = 2 πTL . Выразив из этой формулы TL , имеем:

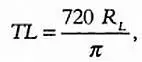
Проведя аналогичные рассуждения и предположив, что Земля вращается вокруг Солнца по окружности радиуса TS ,

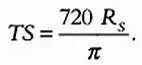
Отношение между расстояниями до Земли и радиусами Луны, Солнца и Земли

Во время лунного затмения Аристарх Самосский заметил, что Луна находится в конусообразной тени Земли в два раза дольше, чем необходимо, чтобы поверхность Луны была полностью покрыта тенью. Он сделал вывод: диаметр конусообразной тени Земли в два раза больше диаметра Луны, таким образом, отношение между этими диаметрами (а следовательно, и радиусами) равно 2:1. Сегодня известно, что отношение радиуса Земли к радиусу Луны равно 2,6:1. Во время лунного затмения с помощью хронометра можно определить отношения интервала между первым и последним соприкосновением границы Луны с конусообразной тенью Земли (этот интервал укажет диаметр конусообразной тени Земли) и интервала, в течение которого поверхность Луны окажется полностью покрыта тенью. Проведя расчеты, нетрудно получить значение, близкое к 2,6:1.

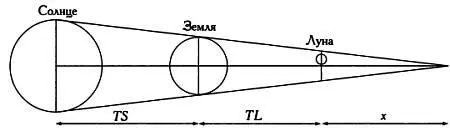
Конусообразная тень Земли и относительное расположение Земли, Луны и Солнца.

Используя обозначения, указанные на иллюстрации, установим следующие соотношения ( х — вспомогательная переменная, которая используется для упрощения расчетов):

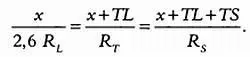
Подставив в эту систему уравнений соотношения T s = 400 T L и R s = 400 R L , исключим вспомогательную переменную х . Упростив выражения, получим:

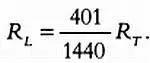
Эта формула позволяет выразить все приведенные выше расстояния через радиус Земли:

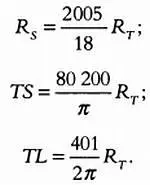
Сюда нужно подставить радиус нашей планеты, чтобы определить все расстояния и радиусы небесных тел в системе «Земля — Луна — Солнце». Аристарху Самосскому не удалось вычислить радиус Земли, следовательно, он получил лишь ряд соотношений, но не расстояния и радиусы в явном виде. Сегодня радиус Земли до экватора известен: он равен 6645 км. Подставив это значение в приведенные выше выражения, получим следующие результаты: R L = 1850 км (реальное значение 1738 км), расстояние TL = 424000 км (реальное значение — 384000 км), R s = 740000 км (реальное значение — 696000 км), расстояние TS = 169600000 км (реальное значение — 149680000 км).

Мы привели эти результаты не для того, чтобы сравнить их с фактическими значениями, а для того чтобы показать, насколько умело действовал грек, получивший настолько точные значения примитивными методами.

Зная точный момент первого и последнего касания границы Луны и конусообразной тени, можно определить диаметр сечения конуса (слева). Зная время, за которое тень покроет поверхность Луны, можно измерить диаметр Луны (справа).

Рассмотрим движение экзопланет вокруг центральной звезды по круговой орбите радиуса а . Приравняем силы, действующие на планету:

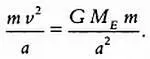
Упростив, получим значение скорости v :

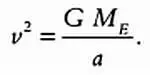
Период Р обращения планеты вокруг звезды по круговой орбите равен:

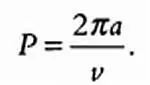
Подставив в это выражение приведенное выше значение скорости v , имеем:

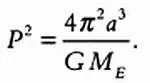
Для каждой экзопланеты можно выразить постоянную, которая приводится в третьем законе Кеплера:

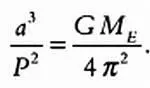
Записав указанное выше соотношение для Земли, период обращения которой вокруг Солнца равен Р = 1 год, а радиус орбиты, которую мы будем считать окружностью, равен а = 1 а. е., получим следующее уравнение:

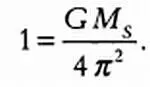
Разделив друг на друга два последних равенства и приняв массу Солнца M s = 1, получим:

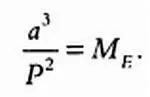
Мы знаем, что а — радиус орбиты (в а. е.), Р — период обращения (в годах), таким образом, мы можем определить массу центральной звезды М E (точнее, отношение ее массы и массы Солнца). Масса центральной звезды в планетной системе М E (относительно массы Солнца) рассчитывается по формуле:

где а — радиус орбиты экзопланеты (в км), Р — период обращения вокруг звезды (в днях). По этой формуле можно вычислить массу звезд Ипсилон Андромеды и Глизе 581 относительно массы Солнца. Полученные значения будут соответствовать приведенным в таблице на странице 60.

Отчасти пожертвовав точностью вычислений, мы попытались упростить математические выкладки и представить достаточно простой и доступный для неспециалистов метод, основанный на гипотезах Галлея и Делиля. Возьмем за основу две гипотезы: будем предполагать, что орбиты Венеры и Земли — это окружности, в центре которых находится Солнце; Венера, центр Солнца и точка, в которой находится наблюдатель на поверхности Земли, лежат в одной плоскости. Будем использовать данные, полученные во время прохождения Венеры по диску Солнца 3 июня 1769 года наблюдателями, расположенными в удаленных друг от друга точках одного и того же меридиана: в норвежском городе Вардё и в Папеэте (Таити) — это две наиболее удаленные друг от друга точки, для которых известны результаты наблюдений. Используем некоторые результаты наблюдений и рассчитаем расстояние от Земли до Солнца.