Роза Мария Рос - Мир математики. т.30. Музыка сфер. Астрономия и математика

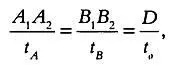
где t A и t B — время прохождения A 1A 2и В 1В 2. Обозначив через t 0 гипотетическое время транзита по всему диску Солнца, через t’ — время, соответствующее Δβ , установим соотношение:

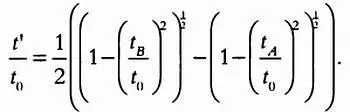
Использовать временные интервалы вместо расстояний следует с осторожностью. Как показано на следующем рисунке, следует различать время внешнего касания ( C 1 и С 4 ) и внутреннего касания ( С 2 и С 3 ) Венеры с диском Солнца. Внутренние касания всегда можно определить точнее, несмотря на искажения, вносимые эффектом черной капли. По этой причине в расчетах учитываются только моменты внутреннего касания.

Наиболее точно можно определить моменты внутреннего касания С 2и С 3, поэтому именно они используются в расчетах.

На основании результатов наблюдений транзита Венеры 1769 года, полученных в Вардё и Папеэте, получим следующие значения (с учетом того, что расстояние АВ по прямой равно 11425 км).

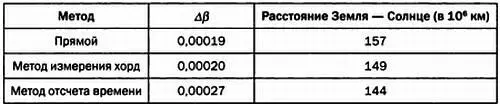
Расстояние от Земли до Солнца, равное 1 астрономической единице, вычисленное тремя описанными выше методами.

Можно видеть, что точность результатов достаточно высока, если принять во внимание простоту использованных методов. Сегодня расстояние от Земли до Солнца, определяемое как 1 астрономическая единица, принимается равным 149,6∙10 6км. Следует отметить, что точность второго результата, полученного методом измерения хорд, выше, так как измерить хорды можно с большей точностью, чем непосредственно Δβ. Последний метод, в котором учитывается время прохождения, представляет интерес, поскольку позволяет провести более четкую аналогию с современными методами. Однако погрешность при этом выше, так как метод требует использования вспомогательной гипотезы, согласно которой скорость движения Венеры во время прохождения по диску Солнца постоянна в течение всего транзита.

Расстояние от Земли до Солнца, вычисленное в XVIII веке, заключалось на интервале от 145 до 155 млн километров. По результатам наблюдений за прохождением Венеры в XIX веке этот результат был улучшен, а максимальная точность была достигнута в 2000 году с помощью радара. Сегодня расстояние от Земли до Солнца принимается равным 149,597870691∙10 6км.

Солнечные часы, как правило, устанавливаются на стенах зданий. Если стена здания не расположена точно вдоль линии восток — запад, часы обычно направлены в сторону горизонта, по которому движется Солнце в течение дня. Чтобы провести часовые линии на циферблате вертикальных неориентированных солнечных часов (они называются наклонными), нужно знать угол, под которым располагается стена. Далее мы объясним, как можно вычислить этот угол а — азимут стены. Пока что будем предполагать, что угол а известен.

Часовые линии в этом случае строятся так же, как и в других разновидностях солнечных часов, то есть путем проецирования часовых линий экваториальных, горизонтальных и вертикальных часов на плоскость циферблата наклонных часов, как показано на иллюстрации. Следует напомнить, что линия, указывающая полдень на циферблате любых вертикальных часов, совпадает с направлением отвеса, закрепленного в той же точке, что и гномон. Гномон наклонных часов, как и любых других солнечных часов, направлен вдоль оси вращения Земли.

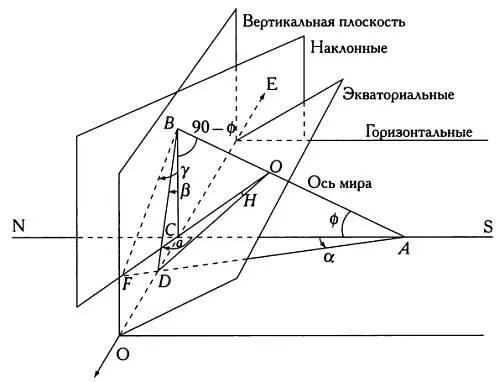
Спроецировав часовые линии экваториальных солнечных часов на плоскость циферблата наклонных часов, получим, что ctg γ= sin a ctg Н sec ф— cos a tg ф. При Н=15°, следовательно, γбудет углом, под которым расположена часовая линия, указывающая 11 и 13 часов. При Н= 30° угол γукажет расположение часовой линии 10 и 14 часов и так далее до линии 6 и 18 часов.

По теореме синусов для треугольника CFA имеем:

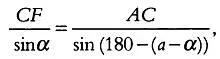
где sin (180 — ( а — α )) = sin ( a — α ) с учетом того, что а и α отсчитываются в противоположных направлениях. По формуле sin ( a — α ) = sina cos α— cosa sin α имеем:

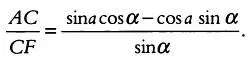
Однако в треугольнике ABC , определяемом осью мира, tg ф = ВС / АС , а в треугольнике BFC на плоскости циферблата наклонных часов tg γ = CF / BC . Упростив эти выражения, получим tg γ tg ф = CF / AC , откуда следует:

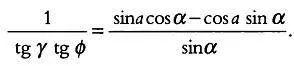
Как мы уже указывали, для горизонтальных часов выполняется равенство tg α = tg Н sin ф , откуда следует:

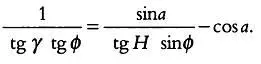
Умножив на tg ф , получим формулу, определяющую положение часовых линий на циферблате наклонных часов:

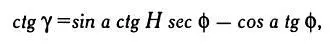
где γ — угол между линией, указывающей 12 часов, и искомой часовой линией, Н = 15°, 30°, 45°… соответственно, как показано на рисунке выше.

Чтобы определить азимут стены, нужно вбить в нее гвоздь, подвесить на него веревку с грузом и использовать пузырьковый уровень, угольник и транспортир, расположив их так, как показано на следующей странице. Измерения нужно производить в солнечный полдень. Азимут стены а — это угол между линией, указывающей на юг, и перпендикуляром к стене. Следует напомнить, что при прохождении Солнца через меридиан места (направление север — юг) тень веревки должна падать строго вертикально.

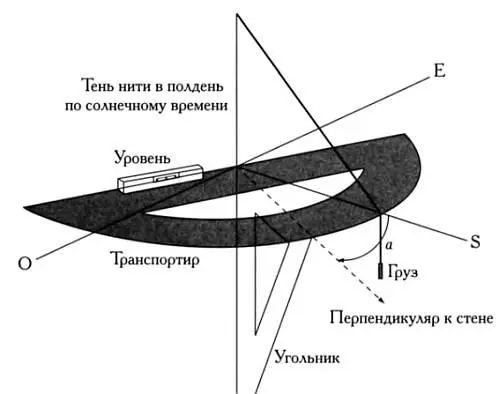
Определение азимута стены а.

Чтобы построить кривую блеска переменной звезды, необходимо произвести множество наблюдений. Каждая точка кривой блеска имеет две координаты ( р, m ), где р — фаза, m — видимая величина.