Генри Дьюдени - 200 знаменитых головоломок мира

От сильного порыва ветра каминная труба сорвалась с крыши и рухнула прямо под ноги случайному прохожему. Он сказал спокойно:

— Мне это ни к чему: я не курю.

Некоторые читатели, увидев головоломку на шахматной доске, склонны сделать столь же невинное замечание:

— Мне это ни к чему: я не играю в шахматы.

Такое отношение в значительной мере результат общераспространенного, но ошибочного убеждения, что обычная шахматная головоломка из тех, которые мы привыкли встречать в периодике (и которые по каким-то соображениям называют задачами), связана с самой игрой в шахматы. Однако в шахматной игре отсутствуют правила, которые обязывали бы нас делать мат в два, три или четыре хода, тогда как большинство позиций в этих головоломках таково, что у одного из игроков (если бы это происходило в реальной шахматной партии) преимущество оказалось бы настолько большим, что другой игрок просто признал бы свое поражение, не доиграв партию до конца. Решение этих головоломок вряд ли поможет вам (да и то косвенным образом) при игре в шахматы; известно, что мастера шахматных головоломок — весьма посредственные игроки, и vice versa [21] Наоборот (лат.). . Если случайно кто-то оказывается силен и в той, и в другой области, то это лишь исключение из правила.

И все же разделенная на клетки доска и ходы шахматных фигур сами по себе весьма примечательным образом приводят к изобретению наиболее занимательных головоломок. Здесь имеется такой простор для всевозможных вариаций, что истинный любитель головоломок не сможет пройти мимо. Именно охраняя интересы тех читателей, которые пугаются одного вида шахматной доски, я публиковал первоначально головоломки этого типа под различными причудливыми одеждами. Одни из этих задач я все еще оставляю в завуалированном виде, другие же я перевел на язык шахматной доски. В большинстве случаев читателю не потребуются вообще никакие познания в области шахмат, но все же для тех, кто не знаком с терминологией, ходами и обозначениями шахматной игры, я ниже дам краткие пояснения.

Сначала мы будем иметь дело с некоторыми вопросами, относящимися к самой шахматной доске, затем — с некоторыми статическими задачами, связанными поочередно с ладьей, слоном, ферзем и конем, затем — с динамическими головоломками, связанными с теми же шахматными фигурами, и, наконец, речь пойдет о смешанных головоломках на шахматной доске. Я надеюсь, что формулы и таблицы, приведенные после статических головоломок, окажутся интересными сами по себе, поскольку публикуются впервые.

Шахматная доска представляет собой квадратную плоскую поверхность, разделенную прямыми линиями, пересекающимися под прямым углом, на 64 квадрата. Первоначально они не были раскрашены поочередно в черный и белый (или какие-либо два других) цвета, и это усовершенствование было введено, просто чтобы помочь глазу при игре. Польза такой раскраски несомненна. Например, она облегчает манипуляции со слонами, позволяя с одного взгляда оценить, что наш король или пешки на черных клетках не находятся под угрозой вражеского слона, передвигающегося по белым клеткам. И все же раскраска шахматной доски несущественна для самой игры как таковой. Точно так же, когда мы формулируем головоломки на шахматной доске, часто неплохо помнить, что дополнительный интерес может представлять «обобщение» на случай доски с любым числом клеток или ограничение задачи некой конфигурацией клеток, необязательно квадратной. Мы приведем несколько головоломок такого типа.

115. Разбивка шахматной доски.Как-то я задался вопросом: сколькими различными способами можно разбить шахматную доску на две части одинаковой формы и размера, если разрезы проводить по границам клеток? Выяснилось, что эта задача одновременно и занимательна и трудна. Я представляю ее в упрощенном виде, взяв доску меньших размеров.

Очевидно, что доску, состоящую из 4 клеток (2 х 2), можно разделить лишь одним способом (прямой, проходящей через центр), ибо повороты и отражения мы не будем рассматривать как новые решения. В случае доски из 16 клеток (4 х 4) существует 6 различных способов. Они все приведены здесь на рисунке, и читателю не удастся найти еще какое-нибудь решение. Теперь возьмите большую доску, 6 х 6, и попытайтесь определить число способов в этом случае.

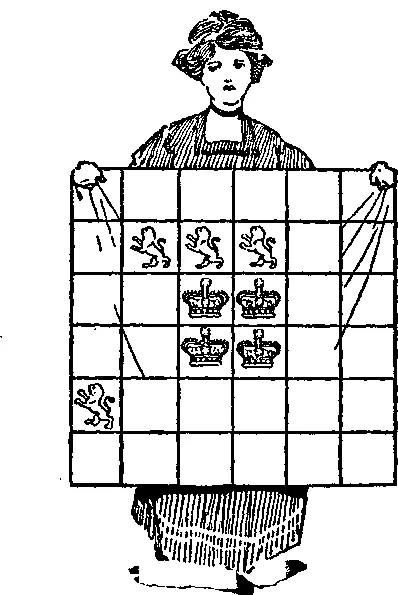
116. Львы и короны. Юная леди, которую вы видите на рисунке, при раскройке столкнулась с небольшой трудностью, помочь преодолеть которую предлагается читателю. По неким причинам, о которых она умалчивает, ей нужно разрезать этот квадратный кусок дорогой ткани на 4 части одинаковых размеров и формы, но важно, чтобы в каждой из частей оказалось по льву и по короне. Поскольку леди настаивает на том, чтобы разрезы пришлись только на границы квадратов, она весьма озадачена. Можете ли вы показать ей нужный способ? Существует только один возможный способ раскройки ткани.

117. Доски с нечетным числом клеток. Рассмотрим доски, которые содержат нечетное число клеток. Начнем с доски 3 х 3. Ее можно разрезать на равные части, лишь удалив центральную клетку.

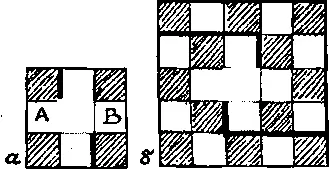
Вполне очевидно, что это можно сделать только одним способом, как показано в случае а. Части А и В имеют одинаковые размеры и форму, и при любом другом способе разрезания получатся такие же части, а, как мы знаем, в подобном случае способы не считаются различными.

Я предлагаю читателю разрезать на две части одинакового размера и формы максимальным числом различных способов доску 5x5 (случай б). На рисунке приведен один из таких способов. Сколько всего существует различных способов? Часть, которая при перевертывании другой стороной кверху принимает ту же форму, что и другая часть, не считается обладающей отличной от нее формой.

118. Задача Великого ламы. Жил некогда Великий лама, у которого была шахматная доска из чистого золота, прекрасно выполненная и, разумеется, огромной ценности. Каждый год в Лхасе среди лам проводился турнир, и тому из них, кому удавалось выиграть у Великого ламы, воздавались большие почести, его имя гравировалось на оборотной стороне доски, а в клетку, где был поставлен мат, вправляли драгоценный камень. После четырех поражений Великий лама умер (возможно, от огорчения).