Майкл Шермер - Магия чисел. Ментальные вычисления в уме и другие математические фокусы

При возведении в квадрат двузначного числа всегда применяется одинаковый метод. Но перемножать двузначные числа можно разными способами, которые в итоге приведут вас к одному и тому же ответу. Лично для меня здесь и начинается самое интересное.

Первый метод, назовем его «метод сложения», можно применять для решения любых задач на умножение типа «2 на 2».

Метод сложения

В методе сложения при перемножении двух двузначных чисел надо всего лишь решить две задачи на умножение типа «2 на 1» и суммировать результаты, например:

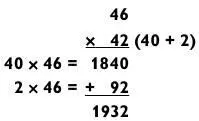
Итак, 42 разбиваем на 40 и 2, после чего умножаем 40 х 46 (а это всего лишь 4 х 46 с добавочным нулем, то есть 1840); затем 2 х 46 = 92. Наконец складываем 1840 + 92 = 1932, как и показано выше.

Вот еще один способ решения той же задачи:

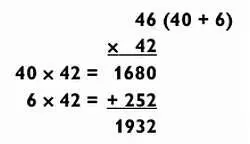
Но здесь есть небольшая проблема, которая заключается в том, что умножить 6 х 42 сложнее, чем 2 х 46, как в первом способе. Более того, прибавить 1680 + 252 сложнее, чем суммировать 1840 + 92. Так как же решить, какое из чисел разбивать на части? Я стараюсь выбирать то, которое приведет к более простой задаче на сложение. В большинстве случаев, но не всегда, желательно разбивать число с наименьшей цифрой в конце, потому что это обычно приводит к меньшим числам при сложении.

Попробуйте свои силы на следующих примерах.

В последнем примере показано, почему числа с 1 в конце лучше всего представлять в виде суммы. В случае если оба числа оканчиваются на одинаковую цифру, следует делить на части большее число, как показано ниже.

Если одно из чисел намного больше другого, то его разбиение часто оправдывает себя, даже если цифра на конце больше цифры на конце меньшего числа. Вы поймете, что я имею в виду, когда решите следующие задачи двумя разными способами.

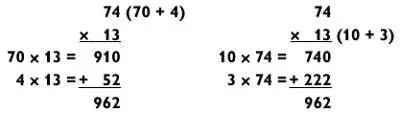
Показался ли вам первый способ быстрее второго? Мне — да.

Вот еще одно исключение из правила: разбивайте на части число с наименьшей цифрой на конце. При умножении числа, близкого и большего 50, на четное, следует разбить на части именно число, близкое к 50.

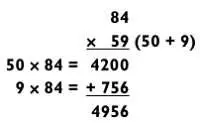
Последняя цифра числа 84 меньше, чем цифра на конце числа 59. Но если разбить на части 59, то результат первого умножения будет кратным 100, что упрощает последующую задачу на сложение.

Теперь попробуйте решить легкую задачу другого типа.

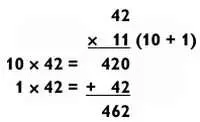
Хотя вычисления, представленные выше, достаточно просты, существует еще более простой и быстрый способ умножения числа на 11. Это магия чисел во всей красе: вы не поверите своим глазам, когда увидите! (Если, конечно, вы еще не забыли, что читали в главе 0.)

Вот как это работает. Представьте себе двузначное число, цифры которого в сумме дают 9 или меньше. Для умножения такого числа на 11 просто сложите эти две цифры и вставьте полученную сумму между двух исходных цифр. Например, чтобы умножить 42 х 11, сначала складываем 4 + 2 = 6. Поместив 6 между 4 и 2, получаем 462, что и является решением!

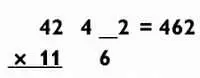
Вычислите 54 х 11, используя данный метод.

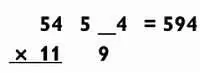
Что может быть проще? Все, что вам нужно, — поставить 9 между 5 и 4 и получить окончательный ответ 594.

Но что делать, когда сумма двух чисел больше 9? В таких случаях надо увеличить цифру десятков на 1, а затем вставить последнюю цифру суммы между двумя числами, как и прежде. Например, при умножении 76 х 11 суммируете 7 + 6 = 13, увеличиваете цифру 7 в числе 76 до 8, а затем вставляете 3 между 8 и 6, что дает окончательный ответ 836.

Посмотрите на схему вычислений:

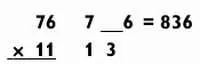
Попытайтесь самостоятельно умножить 68 х 11.

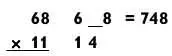
После того как вы освоите этот метод, вы никогда не станете умножать числа на 11 по-другому. Решите несколько задач, а затем сверьтесь с ответами в конце книги.

Следующую задачу вначале бывает очень трудно решить.

Попытайтесь умножить 89 х 72 в уме, подглядывая в случае необходимости в решение. Если вы справились с ней за две попытки, то все в порядке.

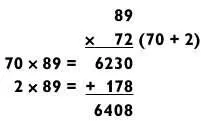
Если вы получили правильный ответ с первого или второго раза, похлопайте себя по плечу. В действительности не найдется задач на умножение типа «2 на 2» труднее этой.

Если вы не получили ответ сразу, не волнуйтесь. В следующих двух разделах я обучу вас более простым стратегиям для решения подобных задач. Но прежде чем продолжить чтение, попрактикуйтесь в методе сложения на следующих задачах на умножение.

Метод вычитания

Метод вычитания может пригодиться, когда одно из умножаемых чисел заканчивается на 8 или 9. Следующий пример показывает, что я имею в виду.

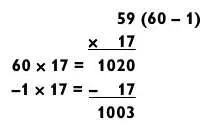
Хотя большинство людей находят, что сложение легче вычитания, порой удобнее отнять маленькое число, чем прибавить большое. (Если бы мы решали эту задачу методом сложения, то пришлось бы складывать 850 + 153 = 1003.)

Теперь рассмотрим сложную задачу, приведенную в конце предыдущего раздела.

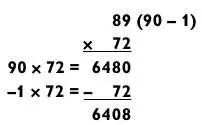
Разве это не намного проще? А вот задача, где одно из чисел заканчивается на 8.