Майкл Шермер - Магия чисел. Ментальные вычисления в уме и другие математические фокусы

Ниже поиск дружелюбного произведения проведен в процессе умножения двумя способами.

43 х 56 = 43 х 8 х 7 = 344 х 7 = 2408.

43 х 56 = 43 х 7 х 8 = 301 х 8 = 2408.

Не показался ли вам второй вариант более легким?

Применяя метод разложения, выгодно отыскивать дружелюбные произведения везде, где только можно. Следующий список должен в этом помочь. Я жду от вас не столько его запоминания, сколько простого ознакомления с ним.

Практикуясь, вы научитесь интуитивно определять дружелюбные произведения, и этот список станет для вас хорошим подспорьем.

Числа с дружелюбными произведениями

12: 12 х 9 = 108.

13: 13 х 8 = 104.

15: 15 х 7 = 105.

17: 17 х 6 = 102.

18: 18 х 6 = 108.

21: 21 х 5 = 105.

23: 23 х 9 = 207.

25: 25 х 4 = 100, 25 х 8 = 200.

26: 26 х 4 = 104, 26 х 8 = 208.

27: 27 х 4 = 108.

29: 29 х 7 = 203.

34: 34 х 3 = 102, 34 х 6 = 204, 34 х 9 = 306.

35: 35 х 3 = 105.

36: 36 х 3 = 108.

38: 38 х 8 = 304.

41: 41 х 5 = 205.

43: 43 х 7 = 301.

44: 44 х 7 = 308.

45: 45 х 9 = 405.

51: 51 х 2 = 102, 51 х 4 = 204, 51 х 6 = 306, 51 х 8 = 408.

52: 52 х 2 = 104, 52 х 4 = 208.

53: 53 х 2 = 106.

54: 54 х 2 = 108.

56: 56 х 9 = 504.

61: 61 х 5 = 305.

63: 63 х 8 = 504.

67: 67 х 3 = 201, 67 х 6 = 402, 67 х 9 = 603.

68: 68 х 3 = 204, 68 х 6 = 408.

72: 72 х 7 = 504.

76: 76 х 4 = 304, 76 х 8 = 608.

77: 77 х 4 = 308.

78: 78 х 9 = 702.

81: 81 х 5 = 405.

84: 84 х 6 = 504.

88: 88 х 8 = 704.

89: 89 х 9 = 801.

Ранее в этой главе вы обучились легкому способу умножать числа на 11. Он применим в методе разложения в ситуации, когда один из множителей равен 11, как в данном примере.

52 х 33 = 52 х 11 х 3 = 572 х 3 = 1716.

83 х 66 = 83 х 11 х 6 = 913 х 6 = 5478.

Я уже упоминал в начале главы, что решать задачи на умножение — одно удовольствие, так как это можно сделать любым количеством способов. Теперь, когда вы поняли, что я имею в виду, применим все три метода, приведенные в этой главе, к одной задаче. Начнем с метода сложения.

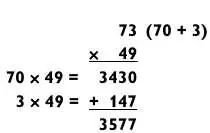
Теперь метод вычитания.

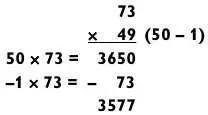
Обратите внимание, что две последние цифры могут быть получены путем сложения 50 + (дополнение для 73), то есть 50 + 27 = 77, или путем вычисления дополнения для разности 73 и 50; дополнение для 23 = 77.

И наконец, метод разложения:

73 х 49 = 73 х 7 х 7 = 511 х 7 = 3577.

Поздравляю! Вы освоили умножение типа «2 на 2» и теперь обладаете всеми необходимыми базовыми навыками для быстрых устных вычислений. Все, что вам нужно для превращения в молниеносного вычислителя, — это больше практики!

УПРАЖНЕНИЕ:

УМНОЖЕНИЕ ТИПА «2 НА 2» ЛЮБЫМ СПОСОБОМ!

У этих упражнений есть несколько вариантов решения. Попробуйте выполнять вычисления столькими способами, сколько вспомните. Затем сверьте свои ответы с данными в конце книги. Наши ответы предлагают различные магические пути решения задач, начиная с самых простых.

Следующие задачи типа «2 на 2» представляют собой подзадачи более сложных задач типа «3 на 2», «3 на 3» и «5 на 5», с которыми вы встретитесь позже. Вы можете решать их сейчас, чтобы поупражняться, а затем снова обратиться к ним, когда они будут включены в большие примеры.

Возведение в квадрат трехзначных чисел — впечатляющее проявление искусности в ментальном фокусничестве. Так же как при возведении в квадрат двузначного числа выполняется его округление в большую или меньшую сторону для получения кратного 10, для возведения трехзначного числа в квадрат его нужно округлить в большую или меньшую сторону для получения кратного 100. Возведем в квадрат число 193.

Путем ок ругления 193 до 200 (второй сомножитель стал равным 186) задача типа «3 на 3» преобразовалась в более простую типа «3 на 1», так как 200 х 186 — это всего лишь 2 х 186 = 372 с двумя нулями в конце. Почти готово! Теперь все, что нужно сделать, это прибавить 7 2= 49 и получить ответ — 37 249.

Попробуем возвести в квадрат 706.

При округлении числа 706 до 700 необходимо еще и изменить это же число на 6 в большую сторону для получения 712.

Так как 712 х 7 = 4984 (простая задача типа «3 на 1»), 712 х 700 = = 498 400. Прибавив 6 2 = 36, получаем 498 436.

Последние примеры не так уж страшны, потому что не включают в себя сложения как такового. Кроме того, вы наизусть знаете, чему равняются 6 2и 7 2. Возводить в квадрат число, которое отстоит от кратного 100 больше чем на 10 единиц, значительно труднее. Попробуйте свои силы с 314 2.

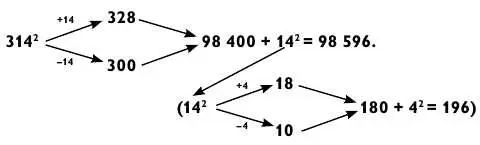
В этом примере число 314 уменьшилось на 14 ради округления до 300 и увеличилось на 14 до 328. Умножаем 328 х 3 = 984 и добавляем два нуля в конце, чтобы получить 98 400. Затем прибавляем квадрат 14. Если вам мгновенно приходит на ум (благодаря памяти или быстрым вычислениям), что 14 2 = 196, то вы в хорошей форме. Далее просто сложите 98 400 + 196 для получения окончательного ответа 98 596.

Если вам нужно время для подсчета 14 2, повторите «98 400» несколько раз, прежде чем продолжить. Иначе можно вычислить 14 2 = 196 и забыть, к какому числу нужно прибавить произведение.

Чем дальше число, возводимое в квадрат, отстоит от кратного 100, тем сложнее становятся вычисления. Попробуйте возвести в квадрат 529.

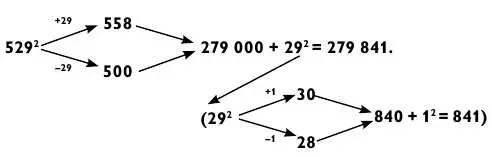
Если у вас есть аудитория, которую вы хотели бы впечатлить, можете произнести вслух «279 000», прежде чем найдете 292. Но такое не пройдет в случае каждой решаемой задачи.

Например, попытайтесь возвести в квадрат 636.

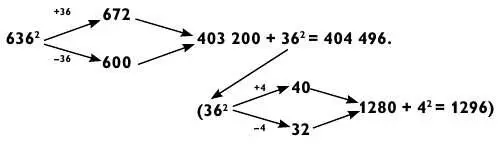
Теперь ваш мозг по-настоящему заработал, не правда ли?