Майкл Шермер - Магия чисел. Ментальные вычисления в уме и другие математические фокусы

Вы уже догадались, что для запоминания чисел от 0 до 5 вам достаточно согнуть нужное количество пальцев на руке. Когда в процесс вовлечен большой палец, будет легко запомнить числа от 6 до 9. Вот список правил большого пальца.

• Чтобы задать 6, поместите большой палец на верхней части мизинца.

• Чтобы задать 7, поместите большой палец на верхней части безымянного пальца.

• Чтобы задать 8, поместите большой палец на верхней части среднего пальца.

• Чтобы задать 9, поместите большой палец на верхней части указательного пальца.

При работе с трехзначным числом задайте цифры для сотен на левой руке и для десятков на правой. Когда дело дойдет до одной цифры, вы достигнете конечной точки решения (за исключением возможного остатка). Теперь произнесите число на левой руке, число на правой руке, последнюю цифру, которую только что посчитали, и остаток (что у вас в голове).

И вот! Вы произнесли ответ!

Чтобы попрактиковаться, попробуйте решить следующую задачу на деление четырехзначного числа.

Пользуясь приемом большого пальца для запоминания ответа, вы зададите 7 на левой руке, соединив большой палец с безымянным, и 6 на правой, соединив большой палец с мизинцем. Как только вычислите последнюю цифру (она равна 3) и остаток (равный 1), можете «зачитать» итоговый ответ с ваших рук слева направо: «семь…шесть…три с остатком один».

Некоторые задачи на деление четырехзначных чисел дают четырехзначный ответ. В таком случае, поскольку у вас только две руки, вам придется вслух произнести цифру для тысячи и использовать правило большого пальца для запоминания остального ответа. Например:

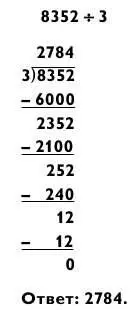
Для решения этой задачи вы делите 8 на 3, чтобы получить цифру 2 для тысяч; произносите «две тысячи» вслух, затем делите 2352 на 3 привычным способом.

В этом разделе мы исходим из предположения, что вы уже освоили искусство деления на однозначные числа. Естественно, задачи на деление с увеличением делителя более сложные.

К счастью, в моем рукаве есть немного магии, чтобы облегчить вам жизнь.

Начнем с относительно простой задачи.

597 ÷ 14

Так как 597 находится между 14 х 10 и 14 х 100, ответ (так называемое частное) лежит между 10 и 100. Чтобы его найти, нужно в первую очередь задать вопрос: «Сколько раз по 14 даст в сумме 590?» Умножив 14 х 40 = 560, вы узнаете, что ответ будет в диапазоне «40 плюс»; так что можно смело произнести вслух «сорок».

Далее вычитаем 560 из 597 и получаем 37, что сводит задачу к делению 37 на 14. Так как 14 х 2 = 28, здесь ответ — 42. Вычитая 28 из 37, мы получаем остаток 9. Процесс решения задачи показан следующим образом.

Следующая задачка немного сложнее, потому что делитель в ней больше.

682 ÷ 23

В данном примере ответ будет двузначным числом, так как 682 находится между 23 х 10 = 230 и 23 х 100 = 2300. Чтобы найти цифру для десятка двузначного числа, нужно подумать: «Сколько раз по 23 даст в сумме 680?» Если вы попробуете 30, то увидите, что здесь незначительный перебор, так как 23 х 30 = 690. Но теперь вы знаете, что ответ лежит в диапазоне «20 плюс» и можете произнести это вслух. Затем вычтите 23 х 20 = 460 из 682, чтобы получить 222. Так как 23 х 9 = 207, ответ — 29 и остаток 222–207 = 15.

Теперь вычислим:

491 / 62

Так как 491 меньше, чем 62 х 10 = 620, ответ будет представлен одной цифрой с остатком. Можно попробовать 8, но 62 х 8 = 496, а это несколько больше делимого. Поскольку 62 х 7 = 434, ответ — 7 и остаток 491–434 = 57, или 7 и 57/62.

Один отличный трюк может облегчить решение таких задач. Помните, как сначала мы пытались перемножить 62 х 8 = 496, но обнаружили, что это число больше, чем нужно? Но это действие оказалось не напрасным. Помимо информации о том, что ответ — 7, оно также позволяет сразу определить остаток.

Поскольку 496 на 5 единиц больше 491, остаток будет на 5 единиц меньше делителя 62. Поскольку 62 — 5 = 57, то ответ — 7 и 57/62. Этот прием работает потому, что 491 = (62 х 8) — 5 = 62 х (7 + 1) — 5 = (62 х 7 + 62) — 5 = (62 х 7) + (62 — 5) = 62 х 7 + 57.

Теперь попробуйте решить пример 380 ÷ 39, используя вышеописанную уловку. Итак, 39 х 10 = 390, что больше делимого на 10. Стало быть, ответ будет 9 с остатком 39–10 = 29.

Следующий вызов для вас — деление четырехзначного числа на двузначное.

3657 / 54

Так как 54 х 100 = 5400, то ответ будет двузначным числом. Для получения первой цифры ответа необходимо выяснить, сколько раз по 54 даст в сумме 3657. Исходя из того что 54 х 70 = 3789 (что немного больше делимого), ответ будет где-то в диапазоне «60 плюс».

Далее умножаем 54 х 60 = 3240 и вычитаем 3657–3240 = 417. Как только вы произнесете «60», ваша задача упростится до 417 ÷ 54. Поскольку 54 х 8 = 432 (что тоже немного больше 417), последняя цифра будет 7 с остатком 54–15 = 39.

Теперь попробуйте свои силы в решении задачи с трехзначным частным:

Упрощение задач на деление

Если к этому моменту ваш мозг уже устал от перенапряжения, расслабьтесь. Как и было обещано, я поделюсь с вами несколькими приемами упрощения задач на деление в уме. Они основаны на принципе деления обеих частей задачи на общий множитель. Если оба числа в примере четные, вы можете вдвойне упростить проблему путем деления каждого числа на 2 перед началом вычислений. Например, задача 858 ÷ 16 содержит два четных числа, и их деление на 2 ведет к значительно более простому действию 429 ÷ 8.

Как видите, остатки 10 и 5 различны; но если записать их в виде дроби, получится 10/16, что равно 5/8. Поэтому в данном методе ответ всегда должен быть представлен в виде дроби.

Мы проделали оба типа вычислений для того, чтобы вы убедились, насколько второй способ легче. Теперь ваша очередь практиковаться:

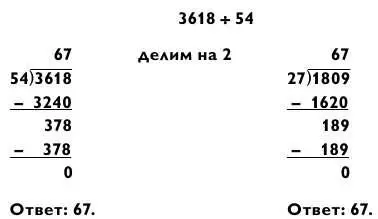
Пример справа гораздо легче решить в уме. Если вы все еще в этом не уверены, можете разделить обе части исходной задачи на 18 для получения еще более простой задачи: 201 ÷ 3 = 67.