Майкл Шермер - Магия чисел. Ментальные вычисления в уме и другие математические фокусы

Высматривайте задачи, которые можно подвергнуть делению на 2 дважды, такие как 1652 ÷ 36.

Мне кажется, что проще дважды разделить числа на 2, чем делить каждое из чисел на 4. Теперь рассмотрим случай, когда оба числа оканчиваются на 0. В этой ситуации можно каждое число разделить на 10.

Если оба числа заканчиваются на 5, удвойте их, а затем разделите на 10 для упрощения задачи. Например:

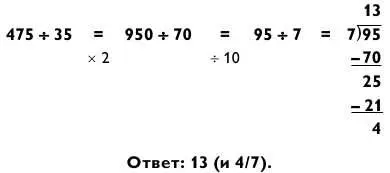
Наконец, если делитель оканчивается на 5, а делимое на 0, умножьте оба на 2, а затем разделите на 10 и далее действуйте так, как мы делали выше.

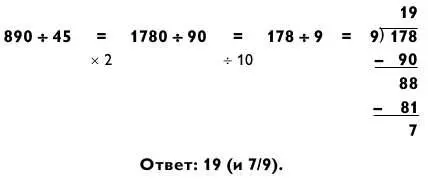
УПРАЖНЕНИЕ: ДЕЛЕНИЕ НА ДВУЗНАЧНЫЕ ЧИСЛА

Здесь вы найдете разнообразные задачи по делению на двузначные числа, которые проверят ваше ментальное мастерство и умение пользоваться простыми техниками упрощения, которые были объяснены в этой главе. Загляните в конец книги для получения объяснений и сверки ответов.

1. 738 ÷ 17

2. 591 ÷ 24

3. 321 ÷ 79

4. 4268 ÷ 28

5. 7214 ÷ 11

6. 3074 ÷ 18

Как вы уже, наверное, догадались, мне нравится заниматься магией, превращая обычные дроби в десятичные. В случае с дробями, в знаменателе которых есть только одна цифра, лучший способ превратить их в десятичные — это почерпнуть их значения из памяти. Это не так сложно, как кажется. Далее вы увидите, что большинство дробей, числители и знаменатели которых представлены однозначными числами (а также 10 или 11), обладают особыми свойствами, поэтому их сложно забыть. Каждый раз, когда вы можете сократить дробь до уже известного вам значения, это ускорит процесс вычислений.

Уверен, вы уже знаете десятичные эквиваленты для следующих дробей:

1/2 = 0,50;

1/3 = 0,333…;

2/3 = 0,666…

Подобно этому

1/4 = 0,25;

2/4 = 1/2 = 0,50;

3/3 = 0,75.

Дроби с пятерками в знаменателе запомнить легче всего.

1/5 = 0,20;

2/5 = 0,40;

3/5 = 0,60;

4/5 = 0,80.

Дроби с шестерками в знаменателе требуют запоминания только двух новых значений.

1/6 = 0,1666…;

2/6 =1/3 = 0,333…;

3/6 = 1/2 = 0,50;

4/6 = 2/3 = 0,666…;

5/6 = 0,8333…

Через мгновение я вернусь к дробям с семерками в знаменателе. А сейчас дроби с восьмерками в знаменателе, преобразовать которые просто элементарно.

1/8 = 0,125;

2/8 = 1/4 = 0,25;

4/8 = 1/2 = 0,50;

6/8 = 3/4 = 0,75;

Дроби с девятками в знаменателе таят в себе особое волшебство.

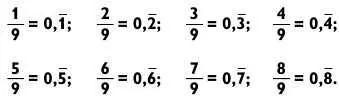
где черта над цифрой обозначает бесконечное повторение этой цифры (говорят, что это дробь в периоде). Например, 4/9 = 0,444…

Дроби с десятками в знаменателе нам уже известны.

1/10 = 0,1; 2/10 = 0,2; 3/10 = 0,3;

4/10 = 0,4; 5/10 = 0,5; 6/10 = 0,6;

7/10 = 0,7; 8/10 = 0,8; 9/10 = 0,9.

Дроби со знаменателем 11 легко вычисляются, если вы запомните, что 1/11 = 0,0909.

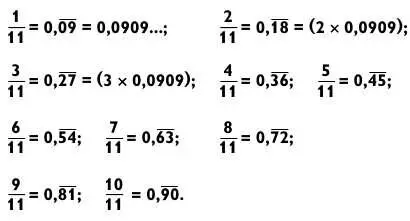
Дроби со знаменателем 7 действительно выдающиеся. Как только вы запомните, что 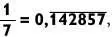то сможете без труда получить значения других дробей с 7 в знаменателе.

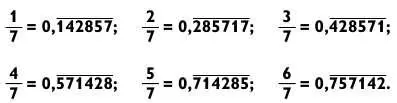
Обратите внимание, что последовательность цифр в периоде циклически повторяется в каждой дроби, при этом изменяется лишь начальная цифра последовательности. Ее можно определить путем умножения 0,14 на числитель дроби.

Например, для дроби 2/7 имеем 2 х 0,14 = 0,28. Поэтому последовательность должна начинаться с 2. Для дроби 3/7 это 3 х 0,14 = 0,42, значит, последовательность начинается с 4.

Другие дроби подчиняются тому же правилу.

Конечно, в процессе решения разнообразных задач вы обязательно столкнетесь с дробями, превышающими 10/11. Поэтому постоянно обдумывайте способы упрощения таких задач. Например, можно упростить дробь 18/34 путем деления числителя и знаменателя на 2, чтобы сократить задачу до 9/17 (ее будет легче решить).

Если знаменатель дроби — четное число, можно упростить дробь, уменьшив ее вдвое, даже если числитель нечетный.

Например,

9/14 = 4,5/7

Деление числителя и знаменателя на 2 сведет проблему к дроби с семеркой в знаменателе. Хотя ранее показанная последовательность дробей не предоставляет десятичного варианта для дроби 4,5/7, как только вы начнете считать, заученное число неожиданно всплывет в памяти.

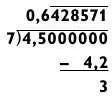
Как видите, вам не пришлось решать задачу целиком.

Стоит вам разделить 3 на 7, и вы точно произведете огромное впечатление на публику, отбарабанив этот длинный набор цифр почти мгновенно! [4] Вычисления происходят следующим образом: 4,5/7 = 4,2/7 + 0,3/7 = 0,6 + 0,1 х 3/7 = 0,6 + 0,1 х 0,428571 = 0,6 + 0,0428571 = 0,6428571. Прим. ред .

Когда делитель заканчивается на 5, то почти всегда умножение на 2, а потом деление на 10 оправдывает себя. Например:

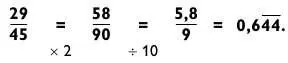
Числа, которые заканчиваются на 25 или 75, надо сначала умножить на 4 и затем разделить на 100.

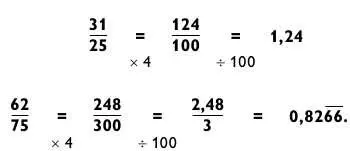
Этот трюк можно применять даже в середине расчетов.

Если вам нужно вычислить дробь 3/16, произойдет вот что:

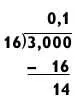
Как только задача сведется к вычислению 14/16, можно привести ее к виду 7/8, что, как известно, равняется 0,875.

Отсюда 3/16 = 0,1875 [5] Здесь вычисления вновь требуют пояснений: 3/16 = 0,1 х 30/16 = 0,1 х 15/8 = 0,1 х (1 + 7/8) = 0,1 + 0,1 х 7/8 = 0,1 + 0,1 х 0,875 = 0,1 + 0,0875 = 0,1875. Прим. ред . .

УПРАЖНЕНИЕ: ПРИВЕДЕНИЕ ДРОБЕЙ К ДЕСЯТИЧНОЙ ФОРМЕ