Майкл Шермер - Магия чисел. Ментальные вычисления в уме и другие математические фокусы

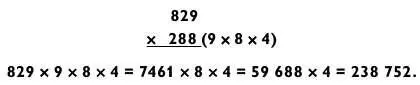
Обратите внимание на последовательность действий. Путем разложения 288 на 9 х 8 х 4 мы упрощаем задачу «3 на 3» (829 х 288) до «3 на 1 на 1 на 1». Далее она превращается в «4 на 1 на 1» (7461 х 8 х 4) и, наконец, в «5 на 1» для получения итогового ответа 238 752. Прелесть данного решения состоит в отсутствии каких-либо действий на сложение и в том, что ничего не нужно хранить в уме. Добравшись до задачи типа «5 на 1», мы оказались в одном шаге от окончательного ответа.

Задачу типа «5 на 1» можно решить в два действия, если представить 59 688 как 59 000 + 688, а затем сложить результаты задач «2 на 1» (59 000 х 4) и «3 на 1» (688 х 4), как показано ниже.

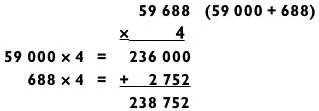
Если оба трехзначных числа можно разложить на «2 на 1», то задача «3 на 3» упрощается до «2 на 2 на 1 на 1», как в следующем примере.

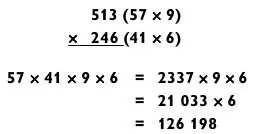
Как обычно, лучше сразу избавиться от трудного элемента задачи, то есть от умножения типа «2 на 2». Как только вы это сделаете, задача будет сведена к «4 на 1», а затем к «5 на 1».

Очень часто бывает так, что раскладывается только один из сомножителей. В таком случае задача сводится к умножению типа «3 на 2 на 1», как в этом примере:

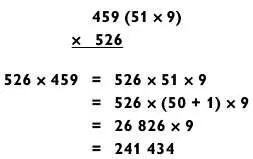
Следующая задача «3 на 3» в действительности просто замаскированная задача типа «3 на 2».

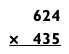
Путем удвоения 435 и уменьшения 624 наполовину получаем эквивалентную задачу.

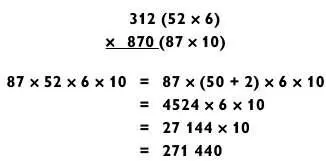
Метод совместной близости

Вы готовы к чему-нибудь попроще? Следующий прием, который был представлен еще в главе 0, основан на такой алгебраической формуле:

(z + a)(z + b) = z

2 + za + zb + ab

Переписываем ее:

(z + a)(z + b) = z(z + a + b) + ab

Эта формула справедлива при любых значениях z , a и b .

Мы будем пользоваться ею всякий раз, когда трехзначные числа, которые нужно перемножить ( z х a и z х b ), находятся близко к легкому числу z (типичный случай, когда число z имеет большое количество нулей). Например, умножим

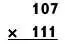
Будем рассматривать эту задачу как (100 + 7) х (100 + 11).

Задав z = 100, a = 7, b = 11, наша формула даст:

100 (100 + 7 + 11) + 7 х 11 = 100 х 118 + 77 = 11 877.

Я схематически изобразил решение так:

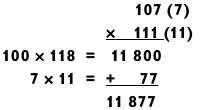
Числа в скобках равны разностям между исходными числами и нашим подходящим «базовым числом» (здесь z = 100).

Число 118 получено путем сложения 107 + 11 или 111 + 7. По законам алгебры, эти суммы эквивалентны, так как (z + a) + b = (z + b) + a.

На этот раз без лишних слов решим еще один «ускоренный» пример:

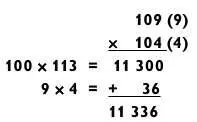
Метод работает великолепно!

Теперь немного повысим ставки и возьмем большее базовое число.

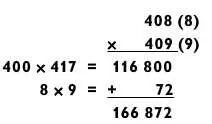
Хотя данный метод, как правило, используется для умножения трехзначных чисел, его также можно применить для задач типа «2 на 2».

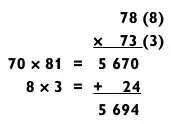
Здесь базовое число 70 умножается на 81 (78 + 3). В таких задачах даже действие на сложение обычно очень простое.

Этот метод также применим, когда оба числа меньше базового. Как, например, в следующей задаче, где оба числа меньше 400.

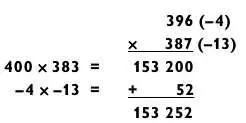
Число 383 получено путем вычитания 396 — 13 или 387 — 4.

Данный метод также можно использовать и для задач типа «2 на 2», таких как следующие.

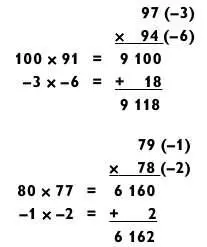
В следующем примере базовое число по величине находится между перемножаемыми числами.

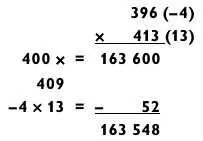
Число 409 получено в ходе операций 396 + 13 или 413 — 4.

Обратите внимание, что, поскольку числа –4 и 13 имеют противоположные знаки, из результата умножения необходимо вычесть 52.

Поднимем ставки еще выше, до уровня, где второе действие требует умножения типа «2 на 2».

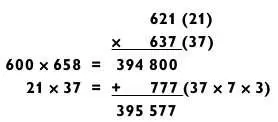
Здесь обратите внимание на то, что первое действие в задаче (600 х 658) является хорошей оценкой ответа. Но наш метод позволяет перейти от оценки к точному ответу.

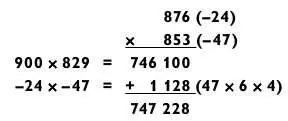
Обратите также внимание, что во всех примерах сумма чисел, которые мы перемножаем в первом действии, такая же, как и исходные числа. Например, в задаче выше 900 + 829 = 1729, как и 876 + 853 = 1729. Это следует из равенства:

z + [(z + a) + b] = (z + a) + (z + b)

Поэтому, чтобы получить число, которое надо умножить на 900 (оно будет в диапазоне «800 плюс»), нужно всего лишь взглянуть на последние две цифры суммы 76 + 53 = 129, чтобы вышло 829.

В следующем примере сложение 827 + 761 = 1588 подсказывает, что нужно перемножить 800 х 788, а затем из полученного результата вычесть произведение 27 х 39.

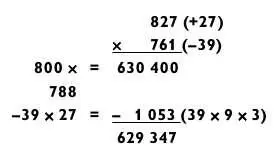
Этот метод настолько эффективен, что если задача типа «3 на 3», над которой вы думаете в настоящий момент, состоит из чисел, далеких друг от друга, то иногда можно видоизменить ее путем деления одного и умножения другого числа на одинаковое число (тем самым сблизив сомножители по величине). Например, задачу 672 х 157 можно решить следующим образом.

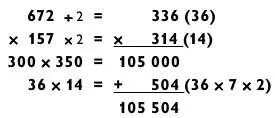
Когда перемножаемые числа одинаковы, метод совместной близости генерирует такие же вычисления, как и в традиционном методе возведения в квадрат.