Майкл Шермер - Магия чисел. Ментальные вычисления в уме и другие математические фокусы

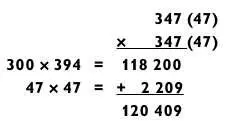
Метод сложения

Когда ни один из предыдущих методов не работает, я ищу возможность использовать метод сложения, в особенности если первые две цифры одного из трехзначных чисел просты в разложении. Например, в нижеприведенном примере 64 (первые две цифры числа 641) раскладывается как 8 х 8, поэтому я его решаю следующим образом.

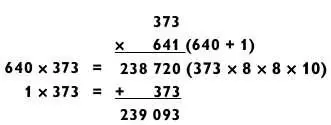
По тому же принципу в примере ниже 42 из числа 427 раскладывается как 6 х 7, поэтому можно использовать метод сложения, представив 427 в виде 420 + 7.

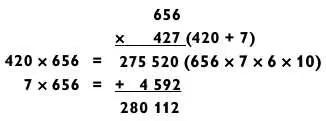
Часто я разбиваю последнюю задачу на сложение на два этапа, как показано ниже.

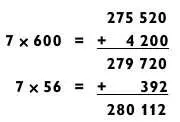
Поскольку задачи, решаемые методом сложения, требуют определенных усилий, обычно я ищу другой способ, который приведет к простым вычислениям в конце процесса решения.

Например, задачу, показанную выше, можно решить с помощью разложения. Вот какие действия я бы выполнил:

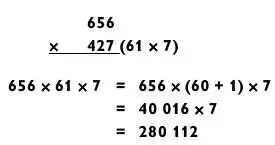
В самых простых задачах, решаемых методом сложения, одно из чисел содержит 0 в середине числа, как показано ниже.

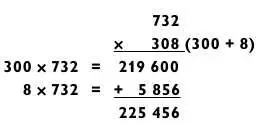
Такие задачи, как правило, самые легкие из тех, которые можно решить аналогичным способом. Поэтому стоит приглядеться к задаче типа «3 на 3», чтобы определить возможность ее преобразования в задачу с нулями. Это окупается.

Например, в задачу 732 х 308 можно преобразовать следующие «безнулевые» примеры.

Мы уже упоминали, что другой способ решения данной задачи сводится к выполнению операций 308 х 366 х 2 и использованию преимущества близости чисел 308 и 366.

Щелкаем еще один «крепкий орешек»:

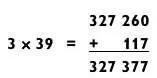
Метод вычитания

Метод вычитания — это орудие, которое я время от времени применяю, когда одно из трехзначных чисел можно округлить до простого трехзначного числа с нулем на конце, как в следующем примере:

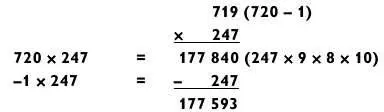
Подобным образом решаем такую задачу:

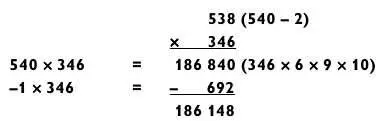
Метод «когда все остальное не работает»

Когда все остальное не срабатывает, я применяю один очень надежный метод. При его использовании задача на умножение типа «3 на 3» разбивается на 3 части: задача типа «3 на 1», типа «2 на 1» и типа «2 на 2». По мере решения этих задач их ответы суммируются. Такие задачи всегда сложные, особенно если нельзя видеть исходные числа. Во время выступлений с задачами на умножение типа «3 на 3» и «5 на 5» у меня всегда под рукой записанные условия, но все расчеты я произвожу в уме.

Вот пример:

На практике вычисления выполняются так, как показано ниже. Иногда я использую фонетический код для хранения в памяти тысяч (здесь 447 = our rug ) и сотен (здесь 1) — на пальцах.

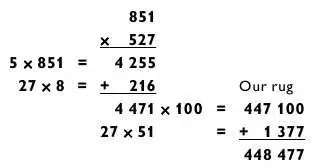
Решим еще один пример, но на этот раз я разобью на части первое число. (Обычно я так поступаю с бóльшим из чисел, так решить задачу на сложение становится легче.)

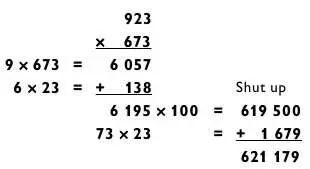
Эти задачи встроены в примеры «5 на 5», которые находятся в следующем разделе.

Самая большая задача, которую мы попытаемся решить в уме, состоит из двух пятизначных чисел. Для выполнения умножения типа «5 на 5» вам необходимо в совершенстве овладеть навыком решения задач типа «2 на 2», «2 на 3» и «3 на 3» (а также уметь применять фонетический код). Решение задачи «5 на 5» — это просто вопрос сведения воедино всех типов задач, освоенных вами ранее. Как и при возведении в квадрат пятизначных чисел, вы будете использовать распределительный закон для разделения чисел на составные части. Например:

Основываясь на этом разделении, данную задачу можно разложить на четыре более простые задачи на умножение в стиле «крест-накрест», что я покажу ниже, как задачу типа «2 на 2», две задачи типа «3 на 2» и одну типа «3 на 3».

Далее суммируются решения всех этих задач. Вот как это выглядит:

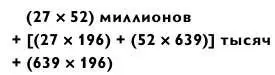
Как и при возведении пятизначных чисел в квадрат, я начинаю с середины, берясь за задачу «3 на 2» (как самую трудную):

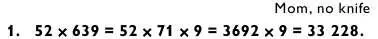
Запомнив число 33 228 с помощью мнемоники Mom, no knife , далее переключаюсь на вторую задачу типа «3 на 2».

2. 27 х 196 = 27 х (200 — 4) = 5400 — 108 = 5292.

И прибавляю этот результат к числу, которое хранится в памяти.

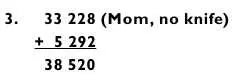
Получаем новую сумму и сохраняем ее в уме как:

Movie lines (38 миллионов, 520 тысяч)

Запомнив этот мнемонический код, решаем задачу «2 на 2».

4. 52 х 27 = 52 х 9 х 3 = 1 404.

На данном этапе уже можно дать частичный ответ. Поскольку задача «2 на 2» — это перемножение миллионов, то 1 404 означает 1 миллиард 404 миллиона. Так как 404 миллиона не подразумевают переноса единицы в разряд миллиардов, то можно спокойно произнести: «Один миллиард…».